| |
| Eléments pour le tracé des courbes paramétrées |
|
Dans tout ce qui suit, on rapporte le plan orienté à un repère orthonormal direct (O,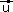 , ,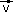 ). L'ensemble des vecteurs du plan est noté V. ). L'ensemble des vecteurs du plan est noté V. |
|
| |
| 1. Vecteur tangent et tangente |
| |
| |
| |
|
| Définition |
Lorsque au point de paramètre t0 le vecteur tangent est non nul, la droite (T) qui passe par M(t0) et de vecteur directeur 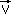 0 est la tangente à la courbe paramétrée au point t0. 0 est la tangente à la courbe paramétrée au point t0. |
|
|
| Remarque : |
D'une manière générale, pour étudier ou tracer une courbe paramétrée, il n'est pas nécesaire de connaître l'équation de la tangente : le vecteur tangent suffit. Si on souhaite connaître l'équation de la tangente, le mieux est d'établir une équation paramétrée de la droite. On sait qu'elle passe par la point M0(f(t0);g(t0)) et que le vecteur directeur est 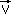 0(f(t0);g(t0)) donc un système d'équations paramétriques de cette tangente est : 0(f(t0);g(t0)) donc un système d'équations paramétriques de cette tangente est : |
|
On élimine ensuite le paramètre t et on obtient une équation cartésienne de (T). |
|
| |
| |
| 2. Symétries et périodicité |
|
Pour retrouver les propriétés suivantes, il est fortement recommandé de faire un schéma, le par-coeur pouvant être source d'erreur ou de confusion. |
Soit I un intervalle de 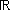 et f et g deux fonctions définies sur I et à valeur dans et f et g deux fonctions définies sur I et à valeur dans 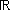 . Dans toute la suite, on définit une courbe paramétrée . Dans toute la suite, on définit une courbe paramétrée 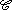 par le système d'équations suivant : par le système d'équations suivant : |
|
|
a. Symétries |
Dans tout le paragraphe, on suppose que l'intervalle I est symétrique, c'est-à-dire que si t appartient à I, alors -t appartient à I : |
|
|
| |
| |
| |
| |
| |
|
| Propriété |
Si pour tout t appartenant à I, on a f(-t) = -f(t) et g(-t) = -g(t) , alors la courbe 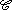 est symétrique par rapport au point O (origine du repère). est symétrique par rapport au point O (origine du repère). |
|
On peut alors réduire de moitié l'intervalle d'étude et étudier la courbe pour les valeur positives (ou négatives) du paramètre, puis compléter la courbe par symétrie centrale de centre O. |
|
| |
| |
| |
| |
| |
|
| Propriété |
Soit 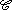 une courbe paramétrée définie par le système d'équations paramétriques suivant : une courbe paramétrée définie par le système d'équations paramétriques suivant : |
|
Si les fonctions f et g admettent une même période T, alors l'étude de la courbe peut être réduite à une étude sur un intervalle du type [t0;t0+T] |
|
| |
| |

