| |
| Définitions et exemples de base |
|
Dans tout ce qui suit, on rapporte le plan orienté à un repère orthonormal direct (O,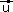 , ,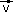 ). L'ensemble des vecteurs du plan est noté V. ). L'ensemble des vecteurs du plan est noté V. |
|
| |
| 1. Définitions |
| |
| |
| |
| |
|
| Remarque : |
Considérons le système d'équations paramétriques suivant : |
|
|
|
On voit que l'on peut obtenir très facilement y = f(x) : les fonctions que nous étudions ne sont en fait que des cas particuliers de courbes paramétrées ! |
|
| |
| 2. Exemples de base |
| |
| |
|
| Exemple : |
Déterminons une équation cartésienne de la droite (D) définie par le système d'équations paramétriques suivant : |
|
On élimine le paramètre t en multipliant la première équation par 2 : |
|
puis en les soustrayant : |
2x - y = 1 |
donc une équation cartésienne de la droite (D) est y = 2x - 1 . |
|
|
| |
|
| Formule Cercle paramétré |
Soit a, b et R réels. Tout système d'équations paramétriques de la forme : |
|
représente un cercle de centre (a,b) et de rayon R . |
|
|
| Démonstration : |
Tout d'abord on isole dans chaque équation les fonctions trigonométriques : |
|
puis on élève au carré : |
|
additionons maintenant les deux équations puis factorisons le second membre par R² : |
(x-a)² + (y-b)² = R²cos²(t) + R²sin²(t) |
(x-a)² + (y-b)² = R²[cos²(t) + sin²(t)] |
On applique la relation fondamentale de la trigonométrie ( cos²(t) + sin²(t) = 1 , pour tout t de 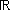 ) et on obtient l'équation cartésienne d'un cercle de centre (a,b) et de rayon R : ) et on obtient l'équation cartésienne d'un cercle de centre (a,b) et de rayon R : |
(x-a)² + (y-b)² = R² |
|
|
| |
|
| Formule Ellipse paramétrée |
Soit a, b réels. Tout système d'équations paramétriques de la forme : |
|
représente une ellipse de centre O, d'axes (O,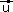 ) et (O, ) et (O,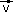 ) et de longueur de demi-axes respectives a et b. ) et de longueur de demi-axes respectives a et b. |
|
|
| Remarque : |
On démontre très facilement ceci en procédant comme pour le cercle : faire apparaitre la relation fondamentale de la trigonométrie. On obtient alors : |
|
|
|
| |

