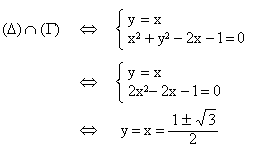Correction du sujet :      Bac S 1999     Maroc  (Juin 99)

Exercice 2  (5 points)                                                           Enoncé

 

            1. a.     1. b.     2. a.     2. b.     2. c.     2. d.    

 

Ce sujet nécessite de connaître les points suivants du cours :

 

 

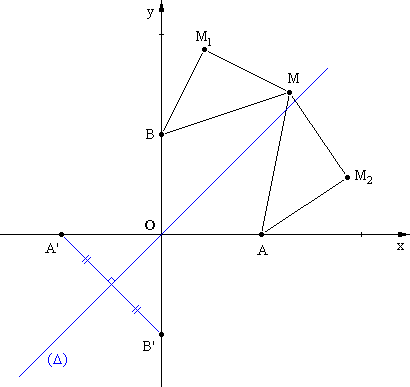
Dans le plan complexe rapporté à un repère orthonormal   ( O ; , )   A , A’ , B , B’ sont les points d’affixes respectives   1 , -1 , i , -i .

 

À tout point M d’affixe z, distinct des points O, A, A', B et B', on associe les points M1 et M2 d’affixes respectives z1 et z2, tels que les triangles BMM1 et AMM2 soient rectangles et isocèles avec :

 

 

Voir la figure sur l’annexe 1, qui sera complétée et rendue avec la copie.

 

1. a. Justifier les égalités   z - z1 = i(i - z1)   et   1 - z2 = i(z - z2) . (0,5 point)

 

Soit M un point quelconque du plan, distinct de O, A, A¢, B et B¢ d’affixe z.

 

On peut utiliser deux méthodes, l'une analytique, l'autre géométrique :

 

 

Le triangle BMM1 est isocèle rectangle en M1 et l’on a :

 

 

On a les affixes suivantes :

 

           

 

Comme le triangle BMM1 est isocèle, on a   M1B = M1M ,

 

donc     |i - z1| = |z - z1|  , d'où :

 

 

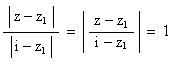
Comme on a :

 

 

 

 

 

 

 

donc on a bien     z - z1 = i (i - z1)  .

 

 

 

 

Le triangle BMM1 est isocèle rectangle en M1 ,

 

donc   M1B = M1M   et les droites (MB) et (M1M) sont perpendiculaires,

 

donc M est l'image de B par la rotation de centre M1 et d'angle p/2 ,

 

On a :

·         z1 est l'affixe de M1 , centre de la rotation

·         i   et   z    sont les affixes respectives de B et M

·         l'angle de la rotation est   p/2 .

 

On sait alors que l'on peut écrire :                  i - z1 = eip/2 (z - z1)

 

donc     z - z1 = i (i - z1)  .

 

 

Exactement avec les mêmes méthodes, en remplaçant M1 par M2  et  B par A , et à partir de l'hypothèse  " BMM2 est isocèle rectangle en M2 " , on montre que :

 

1 - z2 = i (z - z2)  .

 

 

1. b. Vérifier que z1 et z2 peuvent s’écrire : (0,5 point)

 

 

ó        z1 (- 1 + i) = - 1 - z

 

Afin de ne pas garder une expression complexe au dénominateur, nous allons multiplier en haut et en bas par sa quantité conjuguée :

 

 

 

ó        z2 (- 1 + i) = iz - 1 = iz + i² = i(z + i)

 

 

Afin de ne pas garder une expression complexe au dénominateur, nous allons à nouveau multiplier en haut et en bas par sa quantité conjuguée :

 

 

donc on a bien montré que :

 

 

2. On se propose dans cette question de déterminer les points M pour lesquels le triangle OM1M2 est équilatéral.

 

2. a. Montrer que : OM1 = OM2 équivaut à  | z + 1 | = | z + i |  . (1 point)

En déduire l’ensemble (D) des points M tels que OM1 = OM2 et tracer (D) sur la figure. (0,5 point)

 

On a :

 

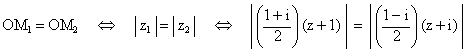
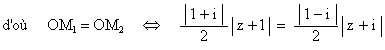
Or        | 1 + i | = | 1 - i |  , car   1 – i    est le conjugué de    1 + i   ,

 

donc    OM1 = OM2 équivaut à   | z + 1 | = | z + i |  .

 

Comme   | z + 1 | = MA’   et   | z + i | = MB’  , on a alors que OM1 = OM2 équivaut à MA’ = MB’  ,

 

donc l’ensemble (D) des points M tels que OM1 = OM2 est la médiatrice de [A’B’] .

 

 

 

2. b. Montrer que : OM1 = M1M2 équivaut à   |z+1|² = 2 |z|²  .   (0,5 point)

 

 

 

 

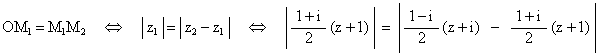
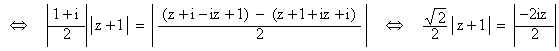
car   | - i | = 1  et en élevant au carré la dernière expression obtenue, on obtient bien :

 

            OM1 = M1M2  ó  | z + 1 |² = 2 | z |²

 

 

2. c. En déduire l’ensemble (G) des points M du plan pour lesquels OM1 = M1M2 . (0,5 point)

On pourra montrer que   |z+1|² = 2.|z|²   équivaut à   |z-1|² = 2   . Tracer (G) sur la figure. (0,5 point)

 

On peut procéder selon deux méthodes distinctes :

 

 

            Posons   z = x + iy    avec x et y réels.

 

On a :   |z + 1|² = |(x + 1) + iy|² = (x + 1)² + y²    et    2 |z|² =  2x² + 2y²  , donc :

 

OM1 = M1M2   ó        |z + 1|² = 2 |z|²

 

                        ó        (x + 1)² + y² = 2x² + 2y²

 

                        ó        x² + 2x + 1 + y² = 2x² + 2y²

 

                        ó        2x + 1 = x² + y²

 

                        ó        1 = x² - 2x + y²

 

                        ó        1 + 1 = x² - 2x +1 + y²

 

                        ó        (x - 1)² + y² = 2   (équation cartésienne de (G), qui est un cercle !)

 

                        ó        |z - 1|² = 2

 

                        ó        AM² = 2

 

L’ensemble (G) des points M du plan vérifiant OM1 = M1M2 est donc le cercle de centre A(1,0) et rayon  .

 

 

 

On sait que le produit d'un nombre complexe par son conjugué est égal au module au carré, donc :

 

 

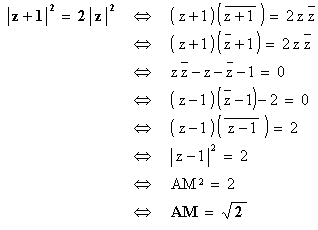
donc l’ensemble (G) des points M du plan vérifiant OM1 = M1M2 est donc le cercle de centre A(1,0) et rayon  .

 

 

 

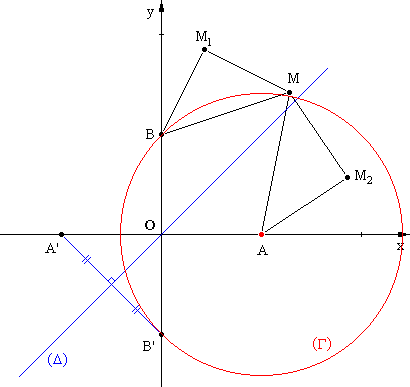
2. d. En déduire les deux points M pour lesquels OM1M2 est un triangle équilatéral et les placer sur la figure. (0,75 point)

 

OM1M2 est un triangle équilatéral signifie que l’on a OM1 = OM2 = M1M2 ,

 

donc   OM1 = OM2   et    OM1 = M1M2  ,

 

donc les points M pour lesquels OM1M2 est un triangle équilatéral appartiennent et à (D) et à (G) ,

 

donc les deux points M pour lesquels OM1M2 est un triangle équilatéral sont les points d’intersection de la droite (D) et du cercle (G).

 

 

Remarque :

 

Il est facile de calculer les coordonnées de ces deux points :

 

On a les équations suivantes :

·         (D) : y = x

·         (G) : (x - 1)² + y² = 2   ó   x² + y² - 2x - 1 = 0

 

d'où :