Correction du sujet : Bac S 1999 Inde (Juin 99)

Problème (11 points) Énoncé

Partie A

Partie B : 1. 2. 3. a. 3. b. 3. c.

Partie C : 1. 2. 3. a. 3. b.

Partie D : 1. 2.

Ce sujet nécessite de connaître les points suivants du cours :

• fonction exponentielle
• équation du type f(x) = 0
• accroissements finis
• suite et récurrence
• intégration

Soit la fonction numérique f définie sur ]0 ; +¥[ par

Partie A : Recherche graphique d’un extremum

L’observation de la courbe représentative de la fonction f sur l’écran graphique d’une calculatrice donne à penser que f admet un minimum sur l’intervalle [0,5 ; 2] .

On se propose d’en donner une valeur approchée.

Observer ci-dessous la représentation graphique de la fonction f ’ , dérivée de f, sur l’intervalle [0,5 ; 2].

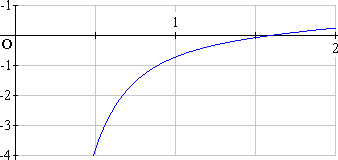
Quels sont les éléments graphiques concernant f ’ qui vont dans le sens de l’existence d’un minimum de f sur [0,5 ; 2] ? (0,5 point)

À l’aide de ce graphique, donner un encadrement d’amplitude 0,2 de l’abscisse de ce minimum. (0,25 point)

La courbe représentative f ’ sur l’intervalle [0,5 ; 2] nous montre que :

• il existe un réel a de [0,5 ; 2] tel que f ’(a) = 0
• cette dérivée est d'abord négative - donc f est décroissante - sur l’intervalle [0,5 ; a]
• cette dérivée est ensuite positive - donc f est croissante - sur l’intervalle [a ; 2]

donc f étant dérivable sur [0,5 ; 2], décroissante sur [0,5 ; a] puis croissante sur [a ; 2], on en déduit l'existence d'un minimum pour f sur [0,5 ; 2].

A partir du graphique, nous pouvons écrire que :

1,5 < a < 1,7.

Partie B : Étude de la fonction F

On considère la fonction h définie sur [0 ; + ¥[ par h(x) = xe^x - 2e^x + 2 .

1. Déterminer les variations de h (on précisera h(0) mais la limite en +¥ n’est pas demandée). (0,5 point)

La fonction h est dérivable sur [0 ; +¥[ en tant que somme de fonctions dérivables sur [0 ; +¥[ .

Pour tout x réel de [0 ; +¥], on a :

h'(x) = e^x + xe^x - 2e^x

= xe^x - e^x

= (x - 1) e^x

Une exponentielle étant toujours positive, le signe de h'(x) est le même que celui de x-1 ,

donc :

• h'(x) > 0 sur [0 ; 1[ , donc h est strictement décroissante sur l’intervalle [0 ; 1[
• h'(1) = 0
• h'(x) < 0 sur ]1 ; +¥[ , donc h est strictement croissante sur l’intervalle [1 ; +¥[ .

On en déduit le tableau de variations suivant pour la fonction h :

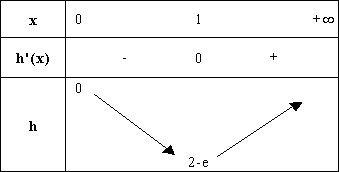
2. Déterminer le signe de h(3/2) . (0,25 point)

En déduire qu’il existe un unique réel a appartenant à l’intervalle [3/2 ; 2] tel que h(a) = 0 . (0,5 point)

En déduire le signe de h sur [0 ; + ¥[. (0,5 point)

On a :

donc h(3/2) » 0,24 ,

donc h(3/2) < 0 .

On a :

• sur [3/2 ; 2] , h est dérivable et strictement croissante donc h réalise une bijection de [3/2 ; 2] sur [h(3/2) ; h(2)]
• h(3/2) < 0
• h(2) = 2+e² > 0

donc l’équation h(x) = 0 admet une unique solution a sur [3/2 ; 2] .

D’après l’étude des variations de h et comme h(0) = 0 , on déduit le tableau de signe suivant :

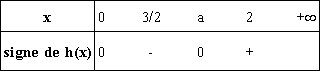
3. Étude de la fonction f

3. a. Calculer les limites de f aux bornes de l’intervalle ]0 ; +¥[. (1 point)

• Pour tout x > 0 , on a :

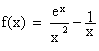
Or

· lim _x®+¥ e^x/x² = +¥ (croissances comparées)

· lim _x®+¥ 1/x = 0

donc par les théorèmes algébriques sur les limites de fonctions, on a :

lim _x®+¥ f(x) = +¥ .

• Pour tout x > 0 , on a :

Or

· lim _x®0+ (e^x-1)/x = 1 (cf. cours)

· lim _x®0+ 1/x = +¥

donc par les théorèmes algébriques sur les limites de fonctions, on a :

lim _x®0+ f(x) = +¥ .

3. b. Montrer que, pour tout nombre x strictement positif : (0,5 point)

En déduire le sens de variation de f et dresser son tableau de variation. (1 point)

Pour calculer la dérivée de f , on va utiliser la formule f ’ = (u/v)’ = (u’v-uv’)/v² , avec :

• u(x) = e^x-1 , d'où u’(x) = e^x
• v(x) = x² , d'où v’(x) = 2x

Pour tout x > 0 , on a donc :

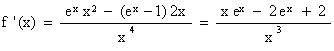
On constate que, pour tout x > 0 , f '(x) = h(x) / x³ ,

et comme x³ > 0 sur ]0 ; +¥[ , f ’(x) est du signe de h(x) sur ]0 ; +¥[ .

donc :

• f ’(x) < 0 sur ]0 ; a[ , d'où f est strictement décroissante sur ]0 ; a[ ;
• f ’(a) = 0 ;
• f ’(x) > 0 sur ]a ; +¥[ , d'où f est strictement croissante sur ]a ; +¥[ .

On déduit de ce résultat le tableau de variation de la fonction f :

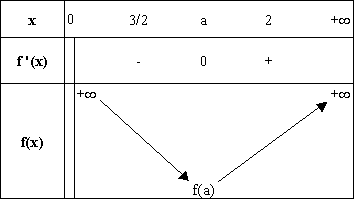
3. c. Montrer que f(a) = -1/[a(a-2)] et en déduire le signe de f(a). (0,5 point ; 0,5 point)

On a :

f '(a) = 0 ó h(a) = 0 (avec a différent de 0 !!)

ó ae^a - 2e^a + 2 = 0

ó e^a = -2/(a-2) (car a est différent de 2 puisque 0 < a < 2 )

donc :

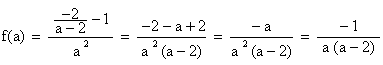
Comme 0 < a < 2 , on a f(a) > 0 .

Partie C : Recherche d’un encadrement de la valeur a

1. Démontrer que, sur [0 ; + ¥[, l’équation h(x) = 0 équivaut à 2(1 - e^-x) = x. (0,5 point)

Sur [0 ; +¥[ , on a :

h(x) = 0 ó xe^x - 2e^x + 2 = 0

ó xe^x = 2(e^x - 1)

ó x = 2(e^x - 1)/e^x (car une exponentielle n'est jamais nulle !)

ó x = 2e^-x(e^x - 1)

ó x = 2(1 - e^-x)

2. Soit la fonction g définie sur [0 ; +¥[ par g(x) = 2(1-e^-x) . On pose I = [3/2 ; 2] .

Montrer que, pour tout x de l’intervalle I , |g'(x)| £ 1/2 . (0,5 point)

La fonction exponentielle étant dérivable et non nulle pour tout x réel, g est dérivable pour tout x de I, d'après les théorèmes de dérivations de fonctions composées.

Pour tout x de I, on a g'(x) = 2e^{- x} .

On a :

3/2 £ x £ 2 ó -2 £ -x £ -3/2 (l'inégalité change de sens car on a multiplié par -1 qui est un nombre négatif)

ó e^-2 £ e^-x £ e^-3/2 (l'inégalité ne change pas de sens car la fonction exponentielle est strictement croissante sur R)

ó 0 < e^-2 £ e^-x £ e^-3/2 (car une exponentielle est toujours strictement positive)

ó 0 < 2e^-x £ 2e^-3/2 (l'inégalité ne change pas de sens car 2 est strictement positif)

Par la calculatrice, on a que 2e^-3/2 » 0,45 ,

donc 2e^-3/2 < 1/2 ,

d'où 3/2 £ x £ 2 ó 0 < 2e^-x < 1/2

donc, pour tout x de I, on a |g'(x)| £ 1/2 .

3. Soit la suite (x_n)_{n > 1} définie pour tout entier n ³ 1 par :

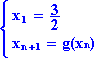
On admet que, pour tout entier n supérieur ou égal à 1, x_n appartient à I.

3. a. Démontrer que, pour tout entier n supérieur ou égal à 1 : (1 point)

En déduire que la suite (x_n) converge vers a. (0,5 point)

On sait que :

• par hypothèse, pour tout entier n ³ 1 , x_n appartient à I ;
• la fonction g est dérivable sur I avec |g'(x)| £ ½ ;

donc, par l'inégalité des accroissements finis, on a :

pour tout y et z de I , |g(y) - g(z)| £ (1/2) |y - z|

Comme

• x_n appartient à I (par hypothèse de l'énoncé) ,
• a appartient à I (cf. question B. 2. ) ,

on peut poser y = x_n et z = a, puis appliquer l'inégalité précédente, on obtient alors :

pour tout entier n ³ 1 , |g(x_n) - g(a)| £ (1/2) | x_n - a|

Or on a :

• g(x_n) = x_n+1
• g(a) = 2(1 - e^-a)

Or par la question B. 3. c. , on a montré que e^a = -2/(a-2) , d'où e^-a = -(a-2)/2 = 1 - (a/2)

donc g(a) = a ,

et on obtient :

Montrons maintenant par récurrence que pour tout entier naturel n ³ 1 , on a : |x_n - a| £ 1/2ⁿ :

• pour n=1, on a : |x₁ - a| = |3/2 - a|

Or, comme a appartient à I, on a :

3/2 £ a £ 2 ó -2 £ -a £ -3/2 (l'inégalité change de sens car on multiplie par -1 qui est négatif)

ó (3/2) - 2 £ (3/2) - a £ (3/2) - (3/2)

ó -1/2 £ (3/2) - a £ 0

ó |3/2 - a| £ 1/2

donc on a bien : |x₁ - a| £ 1/2 et la propriété est bien vraie pour n=1.

• Supposons maintenant cette propriété vraie jusqu'au rang n et montrons la pour le rang n+1 :

On a :

· par hypothèse de récurrence, |x_n - a| £ 1/2ⁿ

· pour tout entier naturel n³1, |x_n+1 - a| £ (1/2) |x_n - a|

donc : | x_n+1 - a| £ (1/2).(1/2ⁿ)

d'où, pour tout entier naturel n³1, |x_n+1 - a| £ 1/2ⁿ⁺¹

donc, par récurrence, on a bien montré que : pour tout entier naturel n ³ 1 , |x_n - a| £ 1/2ⁿ .

Or lim _n®+¥ 1/2ⁿ = 0 ,

donc lim _n®+¥ |x_n - a| = 0 ,

et on déduit de ce résultat que la suite (x_n) converge vers a .

3. b. Déterminer un entier p tel que x_p soit une valeur approchée à 10^-3 près du nombre réel a . (0,5 point)

Donner une valeur approchée de x_p avec trois décimales. (0,5 point)

Un entier p tel que x_p soit une valeur approchée à 10^-3 près du nombre réel a vérifie 1/2^p £ 10^-3 et on a :

1/2 ^p £ 10^-3 ó 2^p ³ 10³

On a 2⁹ = 512 et 2¹⁰ = 1024 ,

donc p=10 est l'entier p tel que x_p soit une valeur approchée à 10^-3 près du nombre réel a ,

donc x₁₀ est une valeur approchée à 10^-3 près du nombre réel a,

On a, à 10^-3 près, x₁₀ = 1,594 .

Partie D : Quelques propriétés d’une primitive de f

On appelle F la primitive de f sur ]0 ; +¥[ qui s’annule en 1. Ainsi l’on a, pour tout réel x de ]0 ; + ¥[

1. Étudier le sens de variation de F sur ]0 ; + ¥[. (0,5 point)

F , primitive de f sur ]0 ; +¥[ , est dérivable pour tout réel x de ]0 ; +¥[, et on a F¢(x) = f(x) .

Or, d'après les résultats de la question B. 3. , comme f(a) > 0, f est strictement positive sur ]0 ; +¥[ ,

donc la fonction F est strictement croissante sur ]0 ; +¥[ .

2. Démontrer que, pour tout x supérieur ou égal à 2 : (0,5 point)

Par comparaison de limites, et en utilisant la relation de Chasles, en déduire lim _x®+¥ F(x) . (0,5 point)

f est strictement croissante sur l’intervalle [2 ; +¥[,

donc pour tout réel t tel que t ³ 2 , on a f(2) £ f(t) .

On a donc pour tout x ³ 2 :

Calcul de la limite de F(x) en +¥ :

Pour tout x>0 , on a :

Or on a montré que, pour tout x ³ 2 , on a :

donc, pour tout x ³ 2 , on a :

Or on a :

On obtient alors :

F(x) ³ F(2) + f(2) (x-2)

Or, comme f(2)>0 , on a lim _x®+¥ f(2)(x-2) = +¥ ,

donc, d'après les théorèmes de comparaison de limites de fonctions, on obtient :

lim _x®+¥ F(x) = +¥ .