Correction du sujet : Bac S 1999 Antilles - Guyane (Juin 99)

Exercice 2 (6 points) Enoncé

1. 2. 3. 4.

Ce sujet nécessite de connaître les points suivants du cours :

• nombres complexes
• applications géométriques

Le plan complexe est rapporté à un repère orthonormal direct (O;,) .

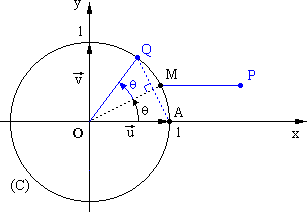
On considère le point A d’affixe 1 et, pour tout q appartenant à [0 ; 2p[, le point M d’affixe z = e^iq.

On désigne par P le point d’affixe 1+z et par Q le point d’affixe z² .

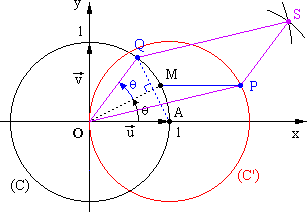
1. À partir du point M, donner une construction géométrique du point P et une construction géométrique du point Q. Les points O, A, M, P et Q seront placés sur une même figure. (1 point)

• L'affixe de P est 1+z ,

donc on passe de M à P en augmentant la partie réelle de l'affixe de M d'une unité,

donc on obtient le point P à partir du point M en faisant une translation de vecteur (1,0) ,

donc P est l'image de M par la translation de vecteur .

• On sait que l'affixe de Q est z² .

Or z = e^iq ,

donc z_Q = z² = e^i2q = e^iq z_M ,

donc le point Q est l’image du point M dans la rotation de centre O et d’angle q (car z_Q = e^iq z_M ) .

2. Déterminer l’ensemble des points P, pour q appartenant à [0 ; 2p[. (1 point)

Tracer cet ensemble sur la figure précédente. (0,5 point)

Nous pouvons procéder suivant deux méthodes différentes : la première est géométrique, la seconde analytique :

1^ère méthode :

On sait que z_M = e^iq ,

donc quand q décrit l'intervalle [0 ; 2p[ , le point M décrit un cercle .

On sait que l'on obtient le point P par une translation de vecteur ,

donc l'ensemble des points P quand q décrit l'intervalle [0 ; 2p[ est l'image par la translation de vecteur du cercle décrit par M .

L'image d'un cercle C de centre O et de rayon R par une translation est un autre cercle, de même rayon R, dont le centre O' est l'image de O par cette translation,

donc l'ensemble des points P quand q décrit l'intervalle [0 ; 2p[ est le cercle (C’) de rayon 1 et de centre A .

2^ème méthode :

Pour q appartenant à [0 ; 2p], nous avons :

z_P = 1 + e^iq = 1 + cos q + i.sin q .

Le point P a donc pour coordonnées :

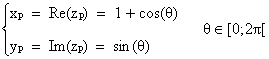
d'où :

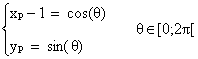
Par la relation fondamentale de la trigonométrie ( sin²(q) + cos²(q) = 1) , on obtient :

.

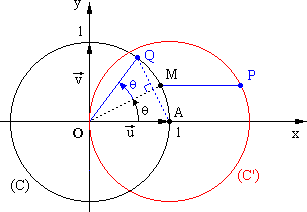
On en déduit que l'ensemble des points P quand q décrit l'intervalle [0 ; 2p[ est le cercle (C’) de rayon 1 et de centre (O,1),

donc il s'agit du cercle de centre A et de rayon 1.

3. Soit S le point d’affixe 1 + z + z², où z désigne toujours l’affixe du point M.

Construire S, en justifiant la construction. (1 point)

On a z_S = 1 + z + z² = (1 + z) + (z²) = z_P + z_Q , donc :

donc on obtient S par cette construction vectorielle et le point S est le quatrième sommet du parallélogramme OPSQ .

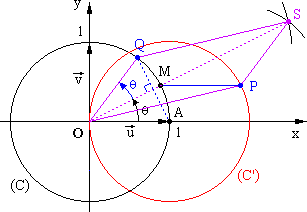
4. Dans le cas où S est différent de O, tracer la droite (OS). Quelle conjecture apparaît, relativement au point M ? (0,5 point)

Démontrer que le nombre (1 + z + z²) / z est réel, quel que soit q appartenant à [0 ; 2p[ . (1 point)

Conclure sur la conjecture précédente. (1 point)

• Conjecture : O, M et S semblent alignés.

• Pour montrer que le nombre (1 + z + z²) / z est réel pour tout q de [0 ; 2p[ , calculons en une autre expression :

donc (1 + z + z²) / z est bien réel pour tout q appartenant à [0;2p[ .

• On déduit de ce qui précède qu'il existe un réel k qui vérifie : (1 + z + z²) / z = k ,

donc (1 + z + z²) = k.z ,

ce qui sous forme vectorielle se traduit par :

donc les points O, S et M sont alignés.

copyright © School Angels 2000