School Angels

Correction du sujet : Bac L 1999 Paris (Juin 99)

Problème (11 points) SPECIALITE Énoncé

Ce sujet nécessite de connaître les points suivants du cours :

exponentielle
solution de l’équation f (x) = 0
étude de courbe
intégration et calcul d’aire

On prendra soin de faire figurer sur la copie les calculs intermédiaires conduisant aux résultats présentés.

Le plan étant rapporté à un repère orthonormal ( O ; i , j) , la courbe (C) tracée sur la feuille annexe représente la fonction f définie sur par :

Le but du problème est d’étudier la fonction f puis d’encadrer une intégrale.

Partie A : Étude d’une fonction auxiliaire g

Soit g la fonction définie sur par g(x) = x + e^x.

1. Calculer la dérivée de g et étudier les variations de g. Déterminer les limites de g en +¥ et en -¥. (0,5 point ; 0,5 point)

La fonction g est dérivable sur , en tant que somme de fonctions dérivables sur .

On a , pour tout x Î , g’(x) = 1 + e^x.

On a, pour tout x Î , e^x > 0 ,

donc, pour tout réel x, g’(x) > 0 .

donc la fonction g est strictement croissante sur .

On a :

lim _x_®₊_¥ x = +¥
lim _x_®₊_¥ e^x = +¥

donc, d’après les théorèmes algébriques de calcul de limite, lim _x_®₊_¥ g(x) = +¥ .

D’autre part :

lim _x_®_-_¥ x = -¥
lim _x_®_-_¥ e^x = 0

donc, d’après les théorèmes algébriques de calcul de limite, lim _x_®_- g(x) = -¥ .

2. Montrer que l’équation g(x) = 0 admet une solution unique a dans et justifier l’encadrement - 0,57 < a < - 0,56 . (0,75 point ; 0,5 point)

g est dérivable et strictement croissante sur ,

donc g réalise une bijection de sur .

D’autre part, lim _x_®₊_¥ g(x) = +¥ et lim _x_®_- g(x) = -¥ ,

donc l’équation g(x) = 0 admet une unique solution a dans .

La calculatrice donne :

g(- 0,57) = - 0,004 à 10^-3 près
g(- 0,56) = 0,011 à 10^-3 près,

donc g(-0,57) < 0 et g(-0,56) > 0 ,

donc, par ce qui précède, on obtient :

- 0,57 < a < - 0,56 .

3. En déduire le signe de g(x) . (0,5 point)

On déduit des résultat obtenus précédemment que :

pour tout x Î ]-¥ ; a[, g(x) < 0 ;
pour tout x Î ]a ; +¥[, g(x) > 0 ;
g(a) = 0 .

Partie B : Étude de la fonction f et de la courbe (C)

1. Sachant que lim _x_®+_¥ e^x/x = +¥ , déterminer la limite de f en +¥.

On admettra que la limite de f lorsque x tend vers -¥ est égale à -¥ (0,25 point)

Pour tout x Î , on a :

On a :

lim _x_®₊_¥ e^x/x = +¥ , donc lim _x_®₊_¥ x/e^x = 0 ,
lim _x_®₊_¥ e^x = +¥ , donc lim _x_®₊_¥ 1/e^x = 0 ,
lim _x_®₊_¥ -x = 0 ,

donc lim _x_®₊_¥ f(x) = -¥ .

2. Montrer que f ’(x) = -g(x)/e^x . Déduire de la Partie A le sens de variation de f. (0,75 point ; 0,5 point)

f est dérivable sur en tant que somme de fonctions quotients dérivables sur (car pour tout x Î , e^x est toujours différent de 0).

Pour tout x Î , on pose :

u(x) = x+1 d’où u’(x) = 1
v(x) = e^x d’où v’(x) = e^x
w(x) = x d’où w’(x) = 1

F étant de la forme f = (u/v) + w , on aura f ’= [(u’v-uv’)/v²] + w’ , d’où :

donc on a bien :

On a, pour tout x Î , e^x > 0 , donc f ‘(x) est du signe de -g(x) .

On déduit alors des résultats de la question A. 2. :

pour tout x Î ]-¥ ; a[, f‘(x) > 0 ;
pour tout x Î]a ; -¥[, f‘(x) < 0 ;
f ’(a) = 0 .

donc :

f est strictement croissante sur ]-¥ ; a[ ;
f est strictement décroissante sur ]a ; -¥[ ;
f admet un maximum en x = a .

On en déduit le tableau de variations suivant pour f :

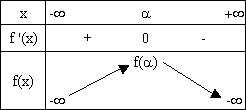
3. En utilisant la question 2. de la Partie A , montrer que f(a) = -1 - a - 1/a . (0,5 point)

a est l’unique solution dans de l’équation g(x) = 0, donc :

g(a) = 0 ó a + e^a = 0 ó e^a= -a .

Donc :

donc :

4. Montrer que la droite (D) d’équation y = -x est asymptote à la courbe (C) en +¥. Étudier la position de (C) par rapport à (D) et préciser les coordonnées de leur point d’intersection. (0,75 point ; 0,75 point).

Pour tout x Î , on a :

D’autre part, on a : (cf. cours)

lim _x_®₊_¥ x/e^x = 0 ;
lim _x_®₊_¥ 1/e^x = 0 .

donc, d’après les théorèmes algébriques, on peut conclure par :

lim _x_®₊_¥ [f(x)-(-x)] = 0

donc la droite (D) d’équation y = -x est asymptote à la courbe (C) au voisinage de +¥ .

Pour tout x Î , f(x) – (-x) = (x+1)/e^x .

Or, pour tout x de , e^x > 0 ,

donc f (x) - (- x) est du signe de (x+1) .

On en déduit que :

pour tout x Î ]-¥ ; -1[, f(x) - (-x) < 0 ;
pour tout x Î]-1 ; +¥[, f(x) - (- x) > 0 ;
pour x = -1, f(x) – (-x) = 0 .

donc :

(C) est au-dessous de (D) sur ]-¥ ; -1[ ;
(C) est au-dessus de (D) sur ]-1 ; +¥[ ;
(C) et (D) se coupe au point de coordonnées (-1 ;1) .

5. Montrer qu’il existe un point A de (C) tel que la tangente en ce point soit parallèle à (D).

Déterminer l’équation de cette tangente que l’on appellera (T). (0,75 point ; 0,5 point)

La tangente à (C) en un point M d’abscisse x est parallèle à (D) si, et seulement si, son coefficient directeur est égal à celui de (D), qui vaut -1 (car (D) : y = -x) .

Le coefficient directeur de la tangente à (C) en M est f ’(x) ,

donc x doit être solution de l’équation f ’(x) = -1 .

On a :

f ’(x) = -1 ó (-x - e^x)/e^x = -1

ó (-x - e^x)/e^x + 1 = 0

ó (-x - e^x + e^x)/e^x = 0

ó -x / e^x = 0

ó x = 0

L’équations de la tangente sera de la forme :

y = f ’(0) ´ (x - 0) + f(0)

y = -x + 1

donc la courbe (C) admet une tangente (T) parallèle à (D) au point A de coordonnées (0 ; 1) et une équation de cette tangente est y = -x + 1 .

6. Construire sur la feuille annexe, qui sera remise avec la copie, les droites (D) et (T). (0,5 point)

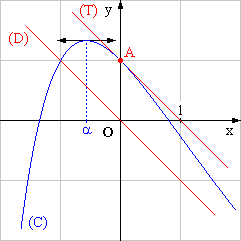
7. En observant la représentation graphique, indiquer quelles semblent être les valeurs de m pour lesquelles l’équation f(x) = - x + m, d’inconnue x, admet une solution unique. (1 point).

On considère la courbe (C) et les droites (D_m) d’équation y = - x + m (où m Î ) . Les solutions de l’équation f(x) = -x + m , d’inconnue x, sont les abscisses des points d’intersections de (C) et (D_m).

(D₀) est la droite (D) et (D₁) est la droite (T) , donc, graphiquement, on remarque que :

si m £ 0 , (D_m) coupe (C) en un seul point, donc l’équation f(x) = -x + m admet une solution unique ;
si 0 < m £ 1 , (D_m) coupe (C) en deux points, donc l’équation f(x) = -x + m n’admet aucune solution.
si m > 1 , alors (D_m) et (C) ne se coupent pas et l’équation

donc l’équation f(x) = -x + m admet une solution unique lorsque m £ 0 .

Partie C : Étude d’une intégrale

On pose :

1. À l’aide d’une interprétation graphique, justifier l’encadrement 1 < J < 2 . (0,5 point)

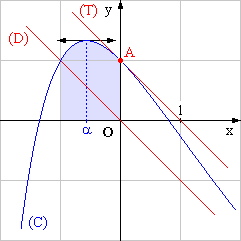
f(-1) = 0 et f(0) = 0 ,

donc, à l’aide du tableau de variations de f , on déduit que f(x) > 0 , pour tout x appartenant à [-1 ; 0] ,

donc J représente l’aire, exprimée en unités d’aire, de la partie de plan limitée par (C), l’axe des abscisses, la droite d’équation x = - 1 et l’axe des ordonnées.

Ce domaine :

contient un carré de côté 1 unité , donc d’aire égale à 1 unité d’aire
est inclus dans un rectangle de côtés 1 et 2 unités, donc d’aire égale à 2 unités d’aires,

donc on a : 1 < J < 2 .

2. a. Calculer la dérivée de la fonction F définie sur par F(x) = (x + 2)e^-x. (0,5 point)

F est dérivable en tant que produit de fonctions dérivables sur .

Posons :

u(x) = x – 2 , d’où u’(x) = 1
v(x) = e^-x , d’où v’(x) = - e^-x .

On peut alors écrire F sous la forme F = uv d’où F ’ = u’v + uv’ .

On a alors, pour tout x Î :

F ’(x) = 1 ´ e^-x + (x - 2) ´ (- e^-x)

= (1 - x - 2)e^-x.

donc F ’(x) = (-x - 1) e^-x .

2. b. En déduire une primitive de f sur . (0,5 point)

Pour tout x Î , on a :

f (x) = (x + 1).e^-x - x = - F ’(x) - x

donc une primitive de f sur est la fonction F₀ définie sur par :

2. c. Calculer la valeur exacte de J. (0,5 point)

Par le résultat de la question précédente on peut alors écrire :

donc :