Correction du sujet : Bac L 1999 Asie (Juin 99)
Exercice
2 (4 points) SPECIALITE Énoncé
Partie A : 1. 2. 3. 4. 5. a. 5. b. 5. c.
Partie B : 1. a. 1. b. 2.
a. 2. b. 2. c. 3.
Ce sujet nécessite de
connaître les points suivants du cours :
- exponentielle
- asymptotes et tangente
- intégration et calcul d’aire
- suite numérique
Partie A :
On considère la fonction f définie
sur ![]() par :
par :
![]()
et on appelle (C) sa courbe dans un repère orthonormal (O ; i , j) d’unité 2 cm.
1. Déterminer les limites de f en +¥ et
en -¥
. (0,5 point)
On a
:
- lim x®+¥ x = +¥ d’où lim x®+¥ (x-1) = +¥
- lim x®+¥ ex = +¥ , d’où
lim x®+¥ (ex +1) = +¥ , d’où
lim x®+¥ 1/(ex +1) =
0 , d’où lim x®+¥ 2/(ex +1) =
0 ,
donc, d’après les théorèmes algébriques de calcul de
limites, on a :
lim x®+¥ f(x) = +¥ .
D’autre part :
- lim x®-¥ x = -¥ d’où
lim x®-¥ (x-1) = -¥
- lim x®-¥ ex = 0
, d’où lim x®-¥ (ex +1) = 1
, d’où lim x®-¥ 1/(ex +1) =
1 , d’où lim x®-¥ 2/(ex +1) =
2 ,
donc, d’après les théorèmes algébriques de calcul de
limites, on a :
lim x®-¥ f(x) = -¥ .
2. Montrer que la droite (D1) d’équation y = x+1 est asymptote à (C) en +¥. (0,5 point)
Préciser la position relative de (C) et de (D1). (0,5 point)
Nous avons, pour tout x de ![]() ,
,
![]()
Or, on a
lim x®+¥ 2/(ex +1) = 0 ,
donc la droite (D1) d’équation y = x - 1
est asymptote à (C) en +¥ .
De plus, on a (comme ex >0 pour tout x
de ![]() )
)
![]()
donc, pour tout x de ![]() , la courbe (C), représentative de f , est
toujours située au-dessus de son asymptote (D1).
, la courbe (C), représentative de f , est
toujours située au-dessus de son asymptote (D1).
3. Montrer que, pour tout réel x, f(x) + f(-x) = 0. (0,5 point)
En déduire que la fonction f est impaire et donner un élément de symétrie de la courbe (C). (0,5 point)
Pour tout réel x ,
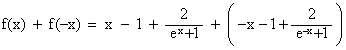
![]()
![]()
![]()
![]()
d’où, pour tout x de ![]() , on a :
f(x) + f(-x) = 0 ,
, on a :
f(x) + f(-x) = 0 ,
donc la fonction f est impaire et sa courbe
représentative (C) est symétrique par rapport au point O , origine du repère.
4. Déduire de ce qui précède que la droite (D2) d’équation y = x+1 est asymptote à (C) en -¥. (0,5 point)
Préciser la position relative de (C) et de (D2). (0,5 point)
On sait que la courbe (C) est symétrique par rapport
au point O , et elle admet en +¥ la droite (D1) pour
asymptote,
donc
par symétrie, la courbe (C) admet une asymptote en -¥ , et cette asymptote est le symétrique de la droite (D1)
par rapport au point O.
Le symétrique de la droite (D1) par
rapport au point O est une droite d’équation
y = x +1 ,
donc la droite (D2) d’équation y = x+1 est
asymptote à (C) en -¥ .
Par symétrie, comme la courbe (C) est au-dessus de
la droite (D1), la courbe (C) est au-dessous de la droite (D2).
5. a. Montrer que, pour tout x : (0,5 point)
![]()
En déduire le sens de variation de f . (0,5 point)
On écrit f sous la forme f = u + 2/v
Avec u et v deux fonctions définies et
dérivables de ![]() dans
dans ![]() par :
par :
- u(x) = x – 1 d’où u’(x) = 1
- v(x) = ex + 1
d’où v’(x) = ex , et la fonction 1/v est également
dérivable sur R car v est dérivable et ne s’annule pas.
f est dérivable sur ![]() en tant que somme de fonctions dérivables sur
en tant que somme de fonctions dérivables sur
![]() , et on a f = u’ + 2(-v’/v2) , d’où :
, et on a f = u’ + 2(-v’/v2) , d’où :
![]()
d’où :
![]()
Pour tout x de ![]() , on a :
, on a :
- ex > 0 , donc e2x > 0 , donc e2x
+ 1 > 0
- (ex + 1)2 > 0
donc pour tout x de ![]() , f ’(x) > 0 ,
, f ’(x) > 0 ,
donc f est strictement croissante sur ![]() .
.
5. b. Déterminer une équation de la tangente (T) à la courbe (C) au point d’abscisse 0. (0,5 point)
La tangente (T) à la courbe (C) au point d’abscisse
0 a pour équation : y = f ’(0) (x–0) + f (0) .
On
a :
- f (0) = 0
- f ’(0) = 1/2
donc l’équation de (T) s’écrit y = x/2
.
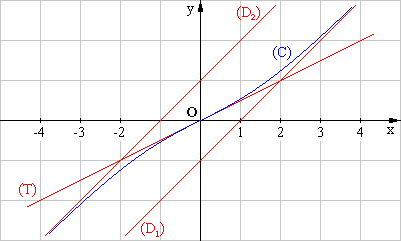
5. c. Tracer dans le repère (O ; i , j) les droites (T), (D1), (D2) et la courbe (C). (1,5 point)
Partie B :
1. a. Démontrer que, pour tout réel x : (0,5 point)
![]()
Pour tout réel x, on a :
![]()
donc on a bien montré que pour tout x réel, f(x)
peut s’écrire :
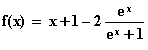
1. b. En déduire l’expression de la primitive F de f , définie sur R, telle que F(0) = - 2 ln(2) . (1 point)
Soit t la fonction définie sur ![]() par t(x) = ex/(ex+1) .
par t(x) = ex/(ex+1) .
t est de la forme z’(x)/z(x) (avec z(x) > 0 sur ![]() ) , donc une primitive de t sera de la forme ln[z(x)] = ln[ex+1] .
) , donc une primitive de t sera de la forme ln[z(x)] = ln[ex+1] .
On en déduit qu’une primitive de f est une fonction
Fk définie sur ![]() et de la forme : (k désigne une
constante réelle)
et de la forme : (k désigne une
constante réelle)
![]()
F est la primitive de f telle que F(0) = -2 ln(2) .
Déterminons la valeur que prend alors la constante k .On a :
Fk(0) = - 2 ln(2)
+ k = -2 ln(2)
d’où k =
0 ,
d’où :
![]()
2. Pour tout entier naturel n, on appelle un l’aire exprimée en cm2 du domaine gn délimité par la courbe (C), la droite (D1) et les droites (Dn) et (Dn+1) d’équations respectives x = n et x = n + 1 .
2. a. Démontrer que, pour tout n : (1 point)
![]()
On a :
1 unité d’aire = 2 ´ 2 = 4 cm2 .
Sur tout ![]() , la courbe (C) est au-dessus de la droite (D1),
donc l’aire un de gn en cm2 est donnée par :
, la courbe (C) est au-dessus de la droite (D1),
donc l’aire un de gn en cm2 est donnée par :
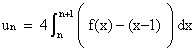
d’où :
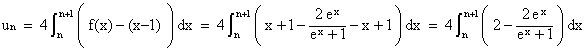
![]()
2. b. Calculer un et montrer que, pour tout n : (1 point)
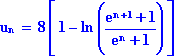
![]()
![]()
![]()
![]()
![]()
d’où :
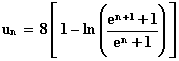
2. c. Représenter sur le graphique les domaines g0 , g1 , g2 ; donner une valeur approchée de u0 à 10-2 près. (1 point)
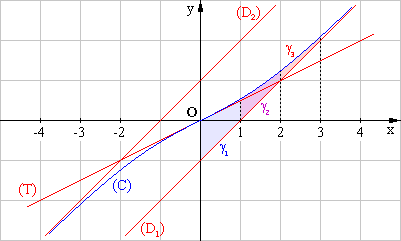
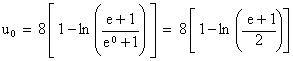
d’où u0 = 3,04 à 10-2 près.
3. Démontrer que, pour tout n :
![]()
et en déduire la limite de (un). (1 point)
On a, pour tout n entier
naturel, en factorisant par en au numérateur et au dénominateur :
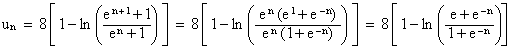
donc on a bien montré que :
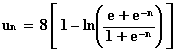
On a lim n®+¥ e n = +¥
donc lim n®+¥ e-n = 0
d’où : lim n®+¥ u
n = 8 [1 – ln(e)]
Or ln(e) = 1
,
d’où lim n®+¥ un = 0 .
copyright © School Angels 2000