School Angels

Correction du sujet : Bac L 1999 Amérique du Nord (Juin 99)

Problème (11 points) SPECIALITE Énoncé

Ce sujet nécessite de connaître les points suivants du cours :

exponentielle
étude de fonction
tangente
intégrales et calcul d’aire

Soit f la fonction définie, pour tout réel x, par f(x) = (- 2x² + 3x) e^x.

Partie A : Étude de f

1. Déterminer les limites suivantes : lim _x_®+_¥ f(x) et lim _x_®-_¥ f(x) (on utilisera lim _x_®-_¥ xⁿe^x = 0 , n entier naturel). (1 point)

On a :

lim _x_®₊_¥ (-2x² + 3x) = -¥ (cf. théorème de limites de polynômes)
lim _x_®₊_¥ e^x= +¥ (cf. cours)

donc, d’après les théorèmes algébriques de calcul de limites, on a :

lim _x_®₊_¥ f(x) = -¥

D’autre part, on a f(x) = -2x².e^x + 3x.e^x ,

Or, d’après l’énoncé, pour tout n entier naturel, on a lim _x_®_-_¥ xⁿe^x = 0 , d’où :

lim _x_®_-_¥ x².e^x = 0
lim _x_®_-_¥ x.e^x = 0

donc, d’après les théorèmes algébriques de calcul de limites, on a :

lim _x_®_-_¥ f(x) = 0

2. Soit f ’ la dérivée de f . Montrer que f ’(x) a le même signe que - 2x² - x + 3 . (1,5 point)

Décomposons f(x) sous la forme f = uv, avec :

u(x) = -2x² + 3x
v(x) = e^x

u et v étant dérivables sur , f est dérivable sur en tant que produit de fonctions dérivables et on a f ’ = u’v + uv’ .

On a :

u(x) = -2x² + 3x d’où u’(x) = - 4x + 3
v(x) = e^x d’où v’(x) = e^x

donc f ’(x) = (- 4x + 3) e^x + (- 2x² + 3x) e^x = (- 2x² - x + 3) e^x .

donc, comme pour tout x e^x> 0 , on obtient que f ’(x) a le même signe que (- 2x² - x + 3) .

3. Étudier le signe de f ’(x) et dresser le tableau de variation de f. (1 point)

On a :

- 2x² - x + 3 = 0 ó x = 1 ou x = -3/2

on en déduit le tableau de signe de f ’(x) :

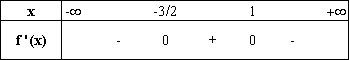
On peut déduire de ce tableau de signe que :

f est décroissante sur ]-¥ ; -3/2[
f est croissante sur ]-3/2 ; 1[
f est décroissante sur ]1 ; +¥[

On peut alors construire le tableau de variations de f :

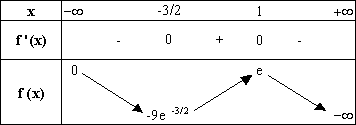
4. Résoudre l’équation f(x) = 0 et étudier la position de (C) par rapport à l’axe des abscisses. (2 points)

f (x) = 0 ó (- 2x² + 3x) e^x = 0

ó - 2x² + 3x = 0 car e^x n’est jamais nul

ó -2x (x – 3/2) = 0

ó x = 0 ou x = 3/2

Les solutions de l’équation f(x) = 0 sont donc 0 et 3/2 .

Un trinôme du second degré de la forme ax² + bx + c étant du signe opposé de celui de a entre ses racines, on en déduit le tableau de signe suivant pour f(x) : (on a donc ici a < 0 !)

Nous déduisons de ce tableau que :

la courbe représentative de f est située au-dessous de l’axe des abscisses pour x appartenant à ]-¥ ; 0[ U ]3/2 ; +¥[ ;
la courbe représentative de f est située au-dessus de l’axe des abscisses pour x appartenant à ]0 ; 3/2[ .

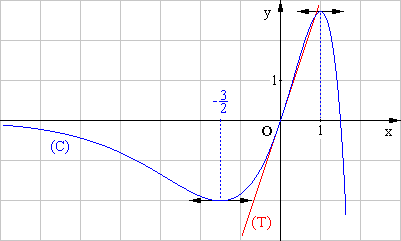
5. Déterminer une équation de la tangente (T) à (C) au point d’abscisse 0. (1 point)

Tracer (T) et (C). (1 point)

On a :

f(0) = 0
f ’(0) = 3

donc une équation de la tangente (T) à la courbe (C) au point d’abscisse x = 0 est :

y = f ’(0) (x–0) + f(0) ,

d’où (T) : y = 3x .

Partie B :

1. On considère les fonctions g et h définies, pour tout x réel, par g(x) = xe^x - e^x et h(x) = x²e^x - 2xe^x + 2e^x.

Calculer les dérivées des fonctions g et h. (1 point)

G et h étant des sommes de produits de fonctions dérivables pour tout x réel , elles sont dérivables sur .

En appliquant les théorèmes de dérivation de somme et de produit de fonctions, on obtient :

g'(x) = e^x + xe^x - e^x d’où g'(x) = xe^x ;
h'(x) = 2xe^x + x²e^x - 2e^x - 2xe^x + 2e^x d’où h'(x) = x²e^x .

2. En utilisant la question 1, calculer : (1 point)

On a :

donc :

D’autre part,

donc :

3. Soit E la partie de plan limitée par l’axe des abscisses, la courbe (C), les droites d’équations x = 0 et x = 3/2 .

En utilisant ce qui précède, donner une valeur numérique décimale approchée à 10^-2 près par défaut de l’aire de E exprimée en cm². (1,5 point)

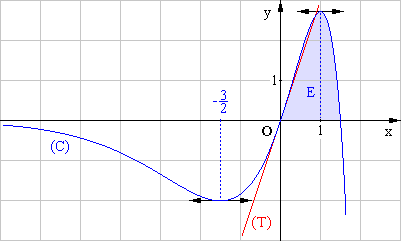
A la question A. 4. , nous avons montré que f(x) ³ 0 sur [0 ; 3/2] , donc l’aire de la portion de plan limitée par la courbe (C) et les droites d’équations x = 0 et x = 3/2 est :

d’où :

L’unité d’aire valant 2 ´ 2 cm² , l’aire A(E) vaut (en cm²) :

d’où A(E) = 10,07 cm² à 10^-2 près.