School Angels

Correction du sujet : Bac ES 1999 Polynésie (Juin 99)

Problème (12 points) Énoncé

Partie A : 1. 2. 3. 4. 5.

Partie B : 1. 2. a. 2. b. 3. 4. 5.

Partie C : 1. 2.

Ce sujet nécessite de connaître les points suivants du cours :

· exponentielle

· étude de fonction

· composée de fonctions

· intégration et calcul d’aire

Le plan est rapporté à un repère orthonormal. On prendra pour unité graphique 2 cm.

On considère les fonctions f et g définies sur l’intervalle [0 ; +¥[ par

Dans le repère choisi, on appelle (C) la courbe représentative de f et (G) la courbe représentative de g.

Partie A :

1. Déterminer la limite de f(x) quand x tend vers +¥ . (0,5 point)

On a :

lim _x_®₊_¥ (x-1) = +¥
lim _t_®₊_¥ e^t = +¥

d’où lim _x_®₊_¥ e^x-1 = +¥ .

De plus, lim _x_®₊_¥ (-x+4) = -¥ ,

d’où lim _x_®₊_¥ (-x+4)e^x-1 = -¥ .

d’où lim _x_®₊_¥ f(x) = -¥ .

2. Vérifier que la fonction dérivée de f est définie pour tout x positif par f ’(x) = (-x+3) e^x-1. (0,75 point)

On définit a et b deux fonctions définies et dérivables sur [0 ; +¥[ :

a(x) = -x + 4 d’où a’(x) = -1
b(x) = e^x-1 d’où b’(x) = e^x-1

On peut alors écrire f sous la forme f = ab et comme a et b sont toutes les deux dérivables sur [0 ; +¥[ , on sait que la dérivée de f s’écrit f ’ = a’b + ab’ d’où :

f ’(x) = -1 ´ e^x-1 + (-x+4) ´ e^x-1

f ’(x) = [(-x+4) – 1] e^x-1

d’où, pour tout x Î [0 ; +¥[ , f ’(x) = (-x+3) e^x-1 .

3. Étudier le sens de variation de la fonction f et dresser son tableau de variation. On précisera f(0) , f ’(0) , f(3) , f ‘(3) . (1,25 point)

On a, pour tout x Î [0 ; +¥[ , f ’(x) = (-x+3) e^x-1 . Or une exponentielle est toujours positive, donc le signe de f ’(x) est celui de (-x+3) , donc :

f ’(x) > 0 sur ]0 ; 3[ ;
f ’(x) < 0 sur ]3 ; +¥[ ;
f ‘(x) = 0 pour x = 3 ;

donc :

f est strictement croissante sur ]0 ; 3[ ;
f est strictement décroissante sur ]3 ; +¥[ ;
f admet un maximum en x = 3 .

On a :

f(0) = 4 e^-1 et f ’(0) = 3 e^-1
f(3) = 3 e² et f ’(3) = 0

On peut alors dresser le tableau de variations de f :

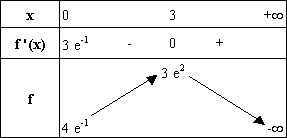
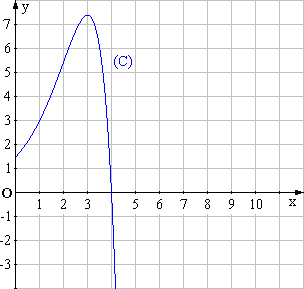
4. Tracer la courbe (C). (1 point)

5. Déterminer les réels a et b tels que la fonction F définie sur l’intervalle [0 ; +¥[ par F(x) = (ax+b) e^x-1 soit une primitive de la fonction f . (1 point)

F est une primitive de f sur [0 ; +¥[ si, et seulement si, pour tout x Î [0 ; + ¥ [ , F ’(x) = f (x) .

Calculons la dérivée de F .

On définit, pour tout x de [0 ; +¥[ , deux fonctions c et d définies et dérivables avec :

c(x) = ax + b d’où c’(x) = a
d(x) = e^x-1 d’où d’(x) = e^x-1

On peut alors écrire F sous la forme F = cd d’où, comme c et d sont dérivables sur [0 ; +¥[ , F est dérivable sur [0 ; +¥[ et on a F’ = c’d + cd’ , d’où :

F’(x) = a e^x-1 + (ax + b)e^x-1

d’où F’(x) = (ax+a+b) e^x-1 pour tout x de [0 ; +¥[ .

On doit avoir F ’(x) = f(x) , pour tout x Î [0 ; +¥[ :

Pour tout x Î [0 ; +¥[ , F ’(x) = f(x) ó (ax+a+b) e^x-1 = (-x+4) e^x-1

ó ax + a + b = -x + 4 (car e^x-1 > 0 pour tout x Î [0 ; +¥[ )

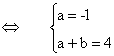
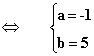
donc la fonction F définie, pour tout x Î [0 ; + ¥[, par F(x) = (x + 5) e^x^-¹ est une primitive de f sur [0 ; + ¥[ .

Partie B :

On considère la fonction u définie sur l’intervalle [0 ; +¥[ par :

1. Vérifier que, pour tout x positif, u(x) est strictement positif. (0,5 point)

Pour tout x Î [0 ; +¥[ , on a :

x + 6 ³ 6 > 0 ;
2x + 2 ³ 2 > 0 ;

donc pour tout x Î [0 ; +¥[ , u(x) > 0 .

2. a. Déterminer la limite de u(x) quand x tend vers +¥ . (0,5 point)

Pour tout x Î ]0 ; +¥[ , on peut écrire :

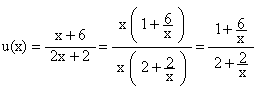
Or on a :

lim _x_®₊_¥ [1 + (6/x)] = 1
lim _x_®₊_¥ [2 + (2/x)] = 2

d’où lim _x_®₊_¥ u(x) = 1/2 .

2. b. Étudier le sens de variation de u . (0,5 point)

Dresser le tableau de variation de u et retrouver le résultat de la question 1. de la Partie B . (0,5 point)

Pour tout x Î [0 ; +¥[ , on définit deux fonctions dérivables e et f par :

e(x) = x + 6 d’où e’(x) = 1
f(x) = 2x + 2 d’où f’(x) = 2

Or :

on peut écrire u sous la forme u = e/f ;
e et f sont dérivables sur [0 ; +¥[ ;
f ne s’annule pas sur [0 ; +¥[ (f(x) = 0 ó x = -2 et -2 Ï [0 ; +¥[ ) ;

donc u est dérivable et on a u’ = (e’f – ef’)/f² , d’où, pour tout x Î [0 ; +¥[ :

Or, pour tout x Î [0 ; +¥[ , (1+x)² > 0 ,

donc u’(x) < 0 pour tout x Î [0 ; +¥[ .

donc u est strictement décroissante sur [0 ; +¥[ .

On déduit de ce qui précède le tableau de variations de u :

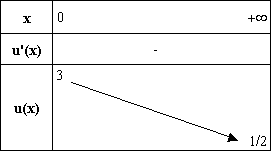
Comme lim _x_®₊_¥ u(x) = 1/2 , et que u est strictement décroissante sur [0 ; +¥[ , on a bien u(x) > 0 sur [0 ; +¥[ .

3. En utilisant les résultats précédents, déterminer le sens de variation de la fonction g et démontrer que la courbe (G) admet une asymptote (D) au voisinage de +¥ dont on donnera une équation. (1 point)

La fonction g est définie, pour tout x Î [0 ; +¥[ , par :

On a :

u est strictement décroissante sur [0 ; +¥[ à valeurs strictement positives ;
la fonction ln est strictement croissante sur ]0 ; +¥[ ;

donc, d’après les théorèmes sur les variations de fonctions composée, g est strictement décroissante sur ]0 ; +¥[ .

On en déduit le tableau de variations de g : (on rappelle que ln(1/2) = - ln(2) )

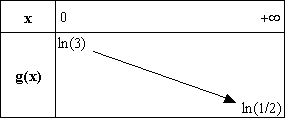
Comme on a lim _x_®₊_¥ g(x) = -ln(2) , la courbe (G) , représentative de g , admet la droite (D) d’équation y = - ln 2 pour asymptote au voisinage de +¥ .

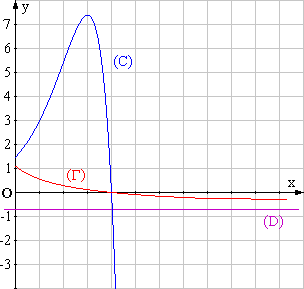
4. Tracer la courbe (G) et la droite (D) sur le même graphique que celui de la partie A . (0,75 point)

5. Soit G la fonction définie sur l’intervalle [0 ; +¥[ par :

G(x) = (x+6) ln(x+6) - (x+1) ln(2x+2) .

Démontrer que G est une primitive de la fonction g sur l’intervalle [0 ; +¥[ . (0,75 point)

Pour tout x Î [0 ; +¥[ , G(x) est dérivable en tant que somme de produits de fonctions dérivables. On a :

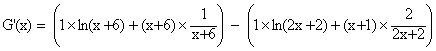
G’(x) = ln(x+6) + 1 - ln(2x+2) – 1

G’(x) = ln(x+6) - ln(2x+2)

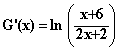
donc pour tout x Î [0 ; +¥[, on a G’(x) = g(x) ,

donc G est une primitive de g sur [0 ; + ¥[.

Partie C :

1. Résoudre, à l’aide des représentations graphiques faites, l’inéquation g(x) £ f(x). (1 point)

La courbe (G) est située au-dessous de (C) sur l’intervalle [0 ; 4] ,

donc l’ensemble des solutions de l’inéquation g(x) £ f(x) est [0 ; 4].

2. Calculer l’aire A en cm² du domaine du plan constitué des points M( x ; y) tels que :

2 £ x £ 3 et g(x) £ y £ f(x) . (1 point)

Donner l’arrondi de A à l’unité près. (1 point)

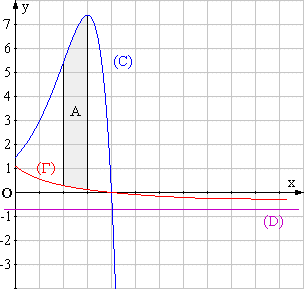
La courbe (G) est située au-dessous de (C) sur [2 ; 3] , donc A s’écrit (en unités d’aires) :

= 2e² - 3e – 9 ln(9) + 4 ln(8) + 8 ln(8) – 3ln(6)

Or on a :

ln(9) = ln(3²) = 2 ln(3)
ln(8) = ln(2³) = 3 ln(2)
ln(6) = ln(2´3) = ln(2) + ln (3)

d’où :

A = 2e² - 3e - 9 ln(9) + 4 ln(8) + 8 ln(8) – 3ln(6)

= 2e² - 3e - 9 ´ [2 ln(3)] + 4 ´ [3 ln(2)] + 8 ´ [3 ln(2)] – 3 ´ [ln(2) + ln(3)]

= 2e² - 3e - 18 ln(3) + 12 ln(2) + 24 ln(2) - 3 ln(2) - 3 ln(3)

A = 2e² - 3e - 21 ln(3) + 33 ln(2) (unités d’aires)

Or une unités d’aire vaut 2 ´ 2 = 4 cm² , d’où :

A = 2e² - 3e - 21 ln(3) + 33 ln(2) (cm²)

A = 26 cm² à 1 cm² près.