| |
| 1. Définition et conséquences |
| |
|
| Définition |
La fonction exponentielle est la fonction, définie sur 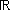 , qui, à chaque réel x, associe le nombre y dont le logarithme népérien est x. , qui, à chaque réel x, associe le nombre y dont le logarithme népérien est x. |
La fonction exponentielle est notée exp ou e suivi d'un exposant . |
|
| |
|
| Propriété |
La fonction exp est dérivable sur 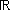 et sa dérivée lui est égale : et sa dérivée lui est égale : |
pour tout x réel, (exp)'(x) = exp(x) |
|
| |
|
| Propriété |
Pour tout x réel, ex > 0 |
Pour tout réel x et pour tout réel y > 0 , on a : y = ex 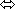 x = ln(y) x = ln(y) |
Pour tout réel x , ln(ex) = x |
Pour tout réel x > 0 , eln(x) = x |
e0 = 1 |
|
| |
| |
| |
| |
| |
| 2. Propriétés algébriques de la fonction exponentielle |
| |
|
| Théorème Relation fondamentale |
Pour tous réels a et b, |
ea+b = ea eb |
|
| |
|
| Propriété |
Pour tous réels a et b, |
ea-b = ea/eb e-b = 1/eb |
|
| |
|
| Propriété |
Pour tous réels a1 , a2 , ... , ap , on a : |
ea1+a2+...+ap = ea1ea2...eap |
|
| |
|
| Propriété |
Pour tout réel a et tout entier relatif k, on a : |
(ea)k = eak |
|
| |
| 3. Dérivation et primitive |
| |
|
| Théorème |
La fonction exp est dérivable sur 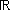 et sa dérivée lui est égale : et sa dérivée lui est égale : |
pour tout x réel, (exp)'(x) = exp(x) |
|
| |
|
Propriété Dérivation de exp u u |
Si u est une fonction dérivable sur un intervalle I, alors la fonction f : x  eu(x) est dérivable sur I et on a : eu(x) est dérivable sur I et on a : |
f '(x) = u'(x).eu(x) |
|
| |
|
| Propriété Primitive |
Si u est une fonction dérivable sur un intervalle I, alors la fonction x  eu(x) est une primitive de la fonction x eu(x) est une primitive de la fonction x  u'(x) eu(x) . u'(x) eu(x) . |
|
|
|
| |
|
| Définition |
Pour tout x réel, on définit le nombre ex ("exponentielle de x") comme étant le nombre dont le logarithme népérien est x : |
ln(ex) = x |
|
|
| |
| 4. Limites utiles |
| |
|
| Propriété (a connaître PAR COEUR) |
|
|
|
|
|
|
| Remarque : |
Pour cette dernière limite, on a : |
|
Il s'agit donc en fait de la forme "limite" de la dérivée de la fonction exponentielle en 0. |
|
| |
| 5. Puissances réelles d'un nombre strictement positif |
| |
|
| Définition |
Pour tous réels a > 0 et b, le nombre "a puissance b", noté ab, est le nombre qui vérifie : |
ab =eb ln(a) |
|
| |
|
| Théorème |
Pour tous réels a et a' strictements positifs et pour tous réels b et b', on a : |
ab = eb ln(a) |
1b = 1 (car ln(1)=0 et e0=1 !) |
(aa')b = ab a'b |
(ab)b' = abb' |
|
|
|
| |

