| |
| 1. Définition |
| |
|
| Definition |
On dit que d est le nombre dérivé de f en a si : |
|
|
| |
|
| Definition |
On dit que d est le nombre dérivé de f en a si : |
|
|
| |
|
| Definition |
On dit que d est le nombre dérivé de f en a si on peut écrire, pour tout réel h tel que a+h soit dans I : |
|
|
| |
| |
|
| Definition |
Lorsque f admet un nombre dérivé en a, on dit que f est dérivable en a . |
Lorsque f est dérivable en tout point de I, on dit que f est dérivable sur I . |
|
| |
| 2. Règles de calcul des dérivées et formulaire |
| |
|
| Formule |
FONCTION | DERIVEE |
a (constante) | 0 |
xn (n  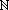 *) *) | n xn-1 |
| |
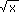 (x > 0) (x > 0) | |
| |
sin x | cos x |
cos x | - sin x |
tan x | 1 + tan² x |
u + v | u' + v' |
uv | u'v + uv' |
| |
| |
un (n  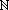 *) *) | n u' un-1 |
f  u u | u' (f ' u) u) |
f(ax+b) | a f '(ax+b) |
|
|
|
|
Remarque : |
Attention de toujours bien vérifier et l'ensemble de définition, et l'ensemble de dérivation, ceux-ci pouvant être différents (par exemple, pour la fonction x  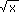 , qui est définie pour x , qui est définie pour x  0 , mais dérivable pour x > 0 . 0 , mais dérivable pour x > 0 . |
Les polynômes, les fractions rationnelles et les fonctions circulaires sont dérivables sur leurs ensembles de définition. |
|
| |
| 3. Sens de variation et extrema locaux |
| |
| |
| |
|
| Théorème |
Soit f une fonction dérivable sur un intervalle I ouvert (c'est-à-dire de la forme ]...;...[ ). |
 si f ' s'annule en un point x0 de I en changeant de signe, alors f admet un extremum local en x0. si f ' s'annule en un point x0 de I en changeant de signe, alors f admet un extremum local en x0. |
 si f admet un extremum local en un point x0 de I, alors f '(x0) = 0 . si f admet un extremum local en un point x0 de I, alors f '(x0) = 0 . |
|
| |
| 4. Dérivation et bijection |
| |
|
| Définition |
Soit I et J deux intervalles. Une bijection de I sur J est une fonction f définie sur I telle que : |
1. pour tout réel x de I, le réel f(x) est dans J ; |
2. pour tout réel c de J, il existe un unique x de I tel que f(x) = c . |
|
| |
|
| Théorème |
Soit f une fonction continue sur un intervalle [a;b] et dérivable sur ]a;b[ : |
 si pour tout x de ]a;b[, f '(x) > 0 , alors f est une bijection de [a;b] sur [f(a);f(b)] ; si pour tout x de ]a;b[, f '(x) > 0 , alors f est une bijection de [a;b] sur [f(a);f(b)] ; |
 si pour tout x de ]a;b[, f '(x) < 0 , alors f est une bijection de [a;b] sur [f(b);f(a)] . si pour tout x de ]a;b[, f '(x) < 0 , alors f est une bijection de [a;b] sur [f(b);f(a)] . |
|
| |
|
| Théorème Très important pour le Bac ! |
|
Soit f une fonction dérivable sur [a;b] . |
Si f ' est de signe constant et si f(a) et f(b) sont de signes contraires, alors l'équation f(x) = 0 admet une unique solution sur ]a;b[ . |
|
|
| Remarque : |
Ce théorème n'est que la conséquence directe du théorème précédent : comme f ' est de signe constant, f est une bijection de I=[a,b] vers J=f([a,b]), puis comme comme 0  J car f(a) et f(b) sont de signes contraires, par définition, il existe un unique réel x de I tel f(x) = 0 , d'où l'existence et l'unicité de la solution. J car f(a) et f(b) sont de signes contraires, par définition, il existe un unique réel x de I tel f(x) = 0 , d'où l'existence et l'unicité de la solution. |
On peut d'ailleurs généraliser pour les équations du type c = f(x) : |
|
| |
|
| Théorème Très important pour le Bac ! |
|
Soit f une fonction dérivable sur [a;b] et c un réel. |
Si f ' est de signe constant et si on a c  [f(a),f(b)] si f(a) < f(b) (ou c [f(a),f(b)] si f(a) < f(b) (ou c  [f(b),f(a)] si f(b) < f(a)) ) , alors l'équation f(x) = c admet une unique solution sur ]a;b[ . [f(b),f(a)] si f(b) < f(a)) ) , alors l'équation f(x) = c admet une unique solution sur ]a;b[ . |
|
| |
| 5. Equation de la tangente à une courbe |
| |
|
| Propriété |
Soit f une fonction définie et dérivable sur un intervalle I et 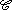 sa courbe représentative. sa courbe représentative. |
La tangente à la courbe C au point de coordonnées (x0,f(x0)) a pour coefficient directeur f '(x0) . |
Une équation de cette tangente est : (elle passe bien sûr par (x0,f(x0)) !) |
y = f(x0) + f '(x0) (x - x0) |
|
|
| Remarque : |
Un rapide calcul permet de vérifier que cette droite passe bien par (x0,f(x0)) , point de contact courbe-tangente . |
|
| |
| 6. Théorème et inégalité des accroissements finis |
| |
|
| Théorème dit "théorème des accroissements finis" |
Soit f et g deux fonction définies et dérivables sur un intervalle I . |
Si pour tout x de I, on a f '(x)  g'(x) , alors pour tout couple de réels a et b de I tel que a < b , on a : g'(x) , alors pour tout couple de réels a et b de I tel que a < b , on a : |
f(b) - f(a)  g(b) - g(a) g(b) - g(a) |
|
| |
| |
| |
|
| Théorème dit "inégalité des accroissements finis avec valeur absolue" |
Soit f une fonction définie et dérivable sur un intervalle I . |
Si il existe un réel M tel que pour tout x de I, on a |f '(x)|  M , alors pour tout couple de réels a et b de I , on a : M , alors pour tout couple de réels a et b de I , on a : |
|f(b) - f(a)|  M|b-a| M|b-a| |
|
| |

