| |
| Représentation et propriétés géométriques des nombres complexes |
|
On rapporte le plan orienté à un repère orthonormal direct (O,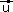 , ,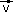 ). L'ensemble des vecteurs du plan est noté V. ). L'ensemble des vecteurs du plan est noté V. |
|
| |
| 1. Image d'un complexe. Affixe d'un point ou d'un vecteur |
| |
|
| Definition |
Pour tout complexe z tel que z = a + ib, on appelle image de z le point M de coordonnées M(a,b) ou encore M(Re(z),Im(z)). |
Pour tout point M du plan, de coordonnées M(a,b), on appelle affixe de M le complexe définit par z = a + ib . |
On note aff(M) l'affixe du point M : aff(M) = a + ib . |
|
|
| Remarque : |
Les points M d'affixe réelle sont les points de l'axe horizontal (O,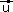 ). ). |
Les points M d'affixe imaginaire pure sont les points de l'axe vertical (O,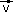 ). ). |
|
| |
| |
|
| Exemples : |
Le point A(3,2) a pour affixe z = 3 + 2i . |
Le complexe z = 3 + 2i a pour image vectorielle 3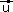 + 2 + 2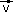 . . |
|
| |
|
| Théorème |
L'affixe de la somme de deux vecteurs est égal la somme de leurs affixes : |
|
|
| |
|
| Théorème |
|
Soient A et B deux points du plan. On a : aff(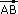 ) = aff(B) - aff(A) ) = aff(B) - aff(A) |
|
| |
| 2. Interprétation géométrique d'opérations algébriques sur les complexes |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |

