

|
Correction du sujet : Bac S 1999
Polynésie (Juin 99)
Exercice
2 (4 points) Enoncé
1. 2. a. 2. b. 2. c. 3. a. 3. b.
Ce sujet nécessite de connaître les points suivants
du cours :
Le plan complexe (P) est rapporté à un
repère orthonormal direct ( O ; u , v ) d’unité graphique 2 cm.
1. Résoudre, dans C, l’équation (E) : z3
- 8 = 0. (0,5 point)
Nous avons :
z3 - 8 = z3 - 23
= (z - 2) (z2 + 2 z +
4)
= (z - 2) [(z + 1)2 +
3]
= (z - 2) [(z + 1)2 - 3i2]
donc on a :
![]()
Pour qu'un produit de facteur soit nul, il faut et
il suffit que l'un des facteurs soit nul,
donc les solutions de l’équation z3 - 8 = 0 sont :
![]()
Remarque :
Au lieu de passer par la forme canonique pour
factoriser, on aurait pu aussi calculer le discriminant du trinôme z2 + 2 z + 4 :
on a D = 2² - 4´1´4= - 12 = 3 (2i)² , puis on
résout avec les formules du cours :
![]()
2. On considère dans le plan (P) les
points A, B et C d’affixes respectives :
![]()
2. a. Écrire zA et zC
sous la forme trigonométrique. (0,5 + 0,5 point)
On reconnaît les racines du polynôme z3 - 8 = 0 .
On a :
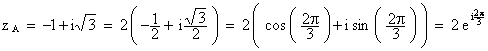
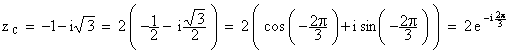
2. b. Placer les points A, B et C. (0,5
point)
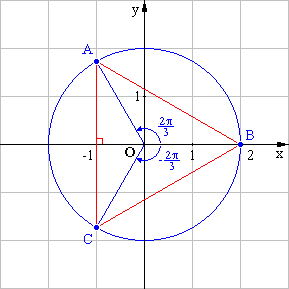
2. c. Déterminer
la nature du triangle ABC. (0,5 point)
Grâce à la figure, on peut s'attendre à ce que le
triangle ABC soit équilatéral. Calculons les longueurs des côtés du triangle :
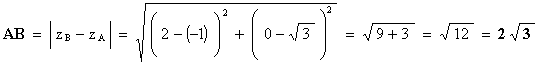
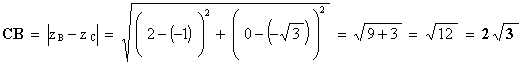
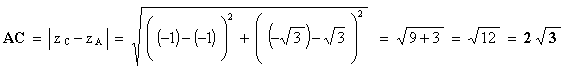
donc AB = AC = BC et le triangle ABC est
équilatéral.
3. On considère l’application f du plan
dans lui-même qui, à tout point M d’affixe z, associe le point M´ d’affixe z'
telle que : z' = e2ip/3 z .
3. a. Caractériser géométriquement l’application
f. (0,5 point)
Par le cours, on sait que la multiplication par un
nombre complexe de module 1 équivaut géométriquement à une rotation de centre O
et d'angle l'argument du complexe considéré,
donc f est la rotation de centre O et d’angle 2p/3 .
3. b. Déterminer les images des points A
et C par f. (0,5 point)
En déduire l’image de la droite (AC) par
f. (0,5 point)
Appelons A'
l’image de A par f. Nous avons :
![]()
donc f(A) =
C .
De même, en appelant C' l'image de C par f, on a :
![]()
donc f(C) =
B .
L’image d