Correction du sujet :      Bac S 1999  Maroc  (Juin 99)

Problème  (11 points)                                                           Enoncé

 

Partie A :        1.         2.         3.         4.

Partie B :        1. a.     1. b.     2. a.     2. b.

Partie C :        1. a.     1. b.     2.         3.         4. a.     4. b.     4. c.     5.

 

Ce sujet nécessite de connaître les points suivants du cours :

 

 

Partie A :   Étude d’une fonction auxiliaire g

 

Soit g la fonction définie sur l’intervalle [0 ; +¥[ par :   g(x) = 2x2 - (x2+1) ln(x2+1) .

 

1. Montrer que g est dérivable sur l’intervalle [0 ; +¥[ et, en détaillant les calculs effectués, montrer que :

 

g’(x) = 2x - 2x ln (x2 + 1). (0,75 point)

 

 

donc   (ln o u) est dérivable sur [0 ; +¥[ .

 

 

On en déduit que g est dérivable sur ]0 ; + ¥[ .

 

On a alors :

 

donc  pour tout x Î [0 ; +¥[,   g'(x) = 2x[1 - ln(x²+1)]  .

 

 

2. Faire l’étude du sens de variation de g sur l’intervalle [0 ; +¥[. (0,5 point)

 

Pour tout x Î [0 ; +¥[ , 2x ³ 0 donc g’(x) est du signe de   1 - ln(x²+1) .

 

On a , pour x ³ 0 :    (on rappelle que la fonction logarithme est croissante donc le sens de l'égalité ne change pas lorsqu'on la fait agir).

 

 

 

 

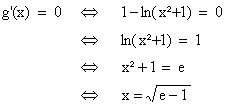
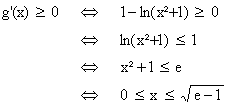
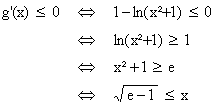
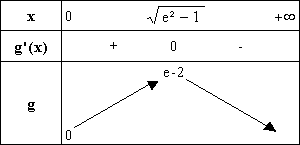
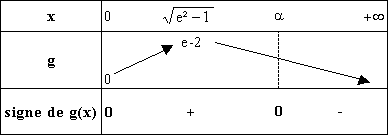
On déduit de ces résultats le tableau de variations de g :

 

 

 

 

3. Montrer que dans l’intervalle  [  ]  , il existe un unique réel a tel que g(a) = 0 ; donner l’approximation décimale à 10- 2 près par défaut de a. (0,75 point)

 

g est dérivable et strictement décroissante sur  [  ] ; g réalise donc une bijection de   [  ]   vers    g ( [  ] )  .

 

Or

 

 

donc l'équation   g(x) = 0   admet une unique solution a dans l'intervalle  [  ] .

 

On a   g(1,98) = 0,00068   et   g(1,99) = -0,023  .

 

L’approximation décimale de a à 10- 2 près par défaut est donc 1,98 .

 

 

4. En déduire le signe de g(x), pour x appartenant à l’intervalle [0 ; + ¥[ . (0,5 point)

 

A partir des résultats précédents, on peut construire le tableau de signe suivant pour g(x) :

 

 

 

 

Partie B :   Étude de la fonction f

 

La fonction f est définie sur [0 ; + ¥[ par :

 

 

Sa courbe représentative (C), dans le plan rapporté à un repère d’origine O, est donnée en annexe, qui sera complétée et rendue avec la copie.

 

1. a. Montrer que lim x®0 f(x)/x = 1 . (0,5 point)

En déduire que f est dérivable en 0 et donner la valeur de f '(0). (0,5 point)

 

En effectuant le changement de variable   h = x² , on a : (quand x tend vers 0, h tend également vers 0)

 

 

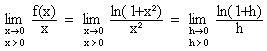
Par le cours, on a   lim h®0 [ln(1+h)]/h = 1 , donc :

 

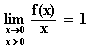
Or on a f(0) = 0 , on peut donc écrire l'expression précédente sous la forme suivante et reconnaître l'expression de la dérivée (à droite) de f en 0:

 

 

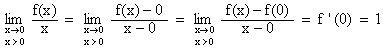
donc     f '(0) = 1 .

 

 

1. b. Vérifier que, pour x strictement positif :   (0,5 point)

Faire l’étude du sens de variation de f sur l’intervalle [0 ; + ¥[. (0,5 point)

 

Pour tout x de ]0 ; +¥[ ,  on a   f = u / v , avec :

 

et on a alors, par le cours,   f ’ = (u’v – uv’)/v² :

 

 

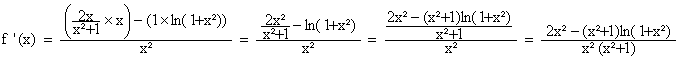
donc pour tout x de ]0 ; +¥[ , on a :

 

Pour tout x de ]0 ; +¥[ ,   on a   x² (1+x²) > 0  ,

 

donc pour tout x de ]0 ; +¥[ , f ’(x)  est du signe de g(x) .

 

A partir des résultats obtenus à la question  A. 4. , on déduit que :

 

donc f est strictement croissante sur [0; a[ et strictement décroissante sur ]a ; +¥[ .

 

 

2. a. Montrer que, pour   x ³ 1 :  (1 point)

 

 

On a pour tout x ³ 1 ,   2x2 ³ x2+1 ³ 1 et on sait que la fonction logarithme népérien est strictement croissante sur ]0 ; +¥[ , donc le sens d'une inégalité est conservé lorsqu'on la fait agir,

 

d'où     ln(x2) ³  ln(x2+1) ³  ln(1) ,

 

On a   ln(1) = 0 ,  et pour tout x ³ 1 , on a    x>0 , donc le sens de l'inégalité ne change pas quand on divise par x , d'où :

 

 

donc pour tout x ³ 1 , on a :

 

 

2. b. En déduire la limite de f en +¥ . (0,5 point)

 

 

On a :

 

donc   lim x®¥ [ln(2x²)]/x = 0   et par le théorème d'encadrement des limites, on a :

 

 

donc   lim x®¥ f(x) = 0  .

 

 

 

Partie C :   Étude d’une primitive de f

 

On note F la primitive de f sur l’intervalle [0 ; + ¥[, qui s’annule pour x = 1    (on ne cherchera pas à calculer F(x) ). On rappelle que :

 

1. a. Montrer que, pour  x > 0 : (0,5 point)

 

Pour tout x > 0, on a :

 

            x2 + 1 ³ x2  ,

 

d'où      ln(x2+1) ³ ln(x2)  , (car la fonction logarithme est strictement croissante pour x>0, donc le sens de l'inégalité est conservé)

 

d'où      ln(x2+1) ³ 2 ln(x) ,

 

 

(le sens de l'inégalité ne change pas car on divise par un nombre strictement positif )

 

Ainsi, pour tout x > 0, on a :

 

 

 

1. b. Calculer I pour x ³ 1 et en déduire la limite de F en +¥ . (1 point)

 

 

On a, pour tout x ³ 1 :

 

 

En posant u(t) = ln(t)  avec  u'(t) = 1/t  , on reconnaît l'intégrale d'une fonction de la forme 2 u' u  , dont une primitive est  u² , d'où :

 

donc on a   I = (ln x)²   .

 

 

 

A la question précédente, on a montré que pour tout x > 0 ,

 

 

donc pour tout x ³ 1 , on a :

 

et comme on a   lim x®¥ [ln(x)]² = +¥ , on a alors :

 

            lim x®¥ F(x) = +¥

 

 

2. Dresser le tableau des variations de F. (0,5 point)

 

Nous avons montré à la question B. 2. que, pour tout x > 0 ,    f(x) > 0  ,

 

et pour tout x ³ 0, on a  F '(x) = f(x) .

 

donc pour tout x ³ 0, F '(x) > 0 et F '(0) = 0 ,

 

donc F est strictement croissante sur [0 ; +¥[ et on a le tableau de variations suivant :

 

 

 

 

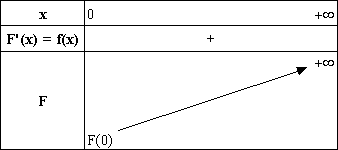
3. Montrer que   f(1) < F(2) < f(a) et en déduire un encadrement de F(2) .  (On prendra f (a) » 0,8.) (0,5 point)

 

L'expression à montrer suggère d'utiliser une comparaison d'intégrale (car F est une primitive de f) .

 

On sait que f(a) est le maximum de f sur [0 ; + ¥[ ,

 

donc pour tout t appartenant à  [1 ; 2], on a :

 

f(1)  £  f(t)  £  f(a)

 

 

 Þ       (2-1) f(1)  £  F(2)  £  (2-1) f(a)

 

donc     f(1) £ F(2) £ f(a) .

 

On a alors à 0,01 près par défaut :

 

            0,69 £ F(2) £ 0,8

 

 

4. On note I le point de coordonnées (1 ; 0), A le point de (C) de coordonnées (1 ; ln 2) et B le point de coordonnées (ln 2 ; ln 2).

4. a. Vérifier que B appartient à la tangente à (C) en O. (0,25 point)

 

L'abscisse de O vaut  0 , donc l'équation de la tangente à (C) en O est :      y = f(0) + f ’(0) (x - 0)

 

Or, on sait que f '(0) = 1  et l’on a  f(0) = 0. (cf.question B. 1.)

 

donc la tangente à (C) au point O a pour équation :   y = x.

 

donc B appartient bien à cette tangente.

 

 

4. b. Placer les points I, A et B sur la figure de l’annexe 1 et tracer les segments [OA], [OB], [BA] et [AI]. (0,25 point)

 

 

 

 

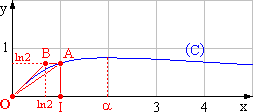
4. c. On admet que, pour les abscisses appartenant à l’intervalle [0 ; 1], la courbe (C) est située au-dessus de [OA] et au-dessous de [OB] et de [BA].

Déterminer un encadrement de F(0), d’amplitude inférieure à 2.10 -1. (0,5 point)

 

On a :

 

On pose :

 

Comme la courbe (C) est située au-dessus de l'axe des abscisses, l'intégrale K représente l'aire, en unités d'aire, de la portion de plan délimitée par (C), l'axe des abscisses, l'axes des ordonnées et la droite d'équation x = 1 .

 

(C) étant située au-dessus de [OA] sur [0 ; 1], donc cette aire est supérieure à l’aire du triangle OAI qui vaut :

 

 

(C) étant située au-dessous de [OB] et de [AB], l’aire représentant K est inférieure à celle du trapèze OIAB, qui vaut :

 

 

On en déduit :

 

 

 

 

 

Avec la calculatrice, on en déduit que :

 

            - 0,5 £ F(0) £ - 0,3

 

 

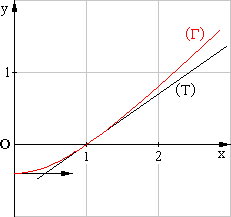
5. Tracer la représentation graphique (G) de F en exploitant au maximum les résultats précédents ; on précisera notamment la tangente à (G) au point d’abscisse 1 en la traçant et en donnant son coefficient directeur. (unité graphique : 2 cm) (1 point)

 

On trace la courbe (G) à partir des informations suivantes :

 

 

 

 

copyright © School Angels 2000