Correction du sujet : Bac S 1999
Paris (Juin 99)
Exercice
2 (5 points) SPECIALITE Énoncé
Ce sujet nécessite de connaître les points suivants
du cours :
- PGCD de deux entiers naturels
- nombres premiers
Partie A :
On admet que 1999 est un nombre premier.
Déterminer l’ensemble des couples
(a ; b) d’entiers naturels admettant pour somme 11994 et pour PGCD 1999.
(1 point)
La question se ramène à la résolution du problème
suivant : trouver a et b tel que
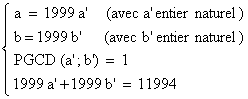
ce qui revient à chercher a' et b' deux entiers
naturels tels que :
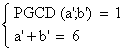
Les solutions de ce système sont (a';b') = (5;1) ou (a';b') = (1;5) ,
d'où on a : (a;b)
= (1999;9995) ou (a;b) = (9995;1999) .
Partie B :
On considère l’équation (E) d’inconnue n
appartenant à N :
(E) : n2 - Sn + 11994 = 0 où S est un entier naturel.
On s’intéresse à des valeurs de S telles
que (E) admette deux solutions dans N.
1. Peut-on déterminer un entier S tel que
3 soit solution de (E) ? (0,25 point)
Si oui, préciser la deuxième
solution. (0,25 point)
3 est solution de (E) ó 9 - 3S + 11994 = 0
ó 3S
= 12 003
ó S
= 4001
donc pour S = 4001, le nombre 3 est solution de (E).
On sait que dans un trinôme du second degré de la
forme x2 + bx + c = 0 :
- -b est égal à la somme des racines
- c est égal au produit des racines
donc l’équation (E) admet pour seconde solution
: n' = 4001 - 3 = 3998 .
2. Peut-on déterminer un entier S tel que
5 soit solution de (E) ? (0,5 point)
5 est solution de (E) ó 25 - 5S + 11994 = 0
ó 5S
= 12019
Comme 12019 n’est pas divisible par 5, il n’existe
pas d’entier S tel que 5 soit solution de (E).
3. Montrer que tout entier n solution de
(E) est un diviseur de 11994. (0,5 point)
En déduire toutes les valeurs possibles
de S telles que (E) admette deux solutions entières. (0,5 point)
n est solution de (E) ó n2
- Sn + 11994 = 0
ó nS
- n2 = 11994
ó n(S-n)
= 11994
et comme n divise
n(S-n) , n doit diviser 11994 .
Chercher les solutions entières de l'équation (E) :
n2 - Sn + 11994 = 0 revient
à chercher les solutions du système d'équations suivant :
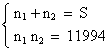
Comme 1999 est un nombre premier (hypothèse de
l'énoncé), la décomposition en facteurs premiers de 11994 est :
11994 = 1999 ´ 3 ´ 2 ´ 1 .
Les solutions entières de n1 n2 = 11994 sont : (la valeur de S est alors indiquée en dernière ligne)
|
n1 |
1 |
2 |
3 |
6 |
1999 |
3998 |
5997 |
11994 |
|
n2 |
11994 |
5997 |
3998 |
1999 |
6 |
3 |
2 |
1 |
|
S = n2
+ n1 |
11995 |
5999 |
4001 |
2005 |
2005 |
4001 |
5999 |
11995 |
Partie C :
Comment montrerait-on que 1999 est un
nombre premier ? Préciser le raisonnement employé. (1 point)
On
peut montrer que 1999 est un nombre premier en utilisant la méthode dite
"du crible d'Ératosthène" : on examine si 1999 est divisible par tous
les nombres premiers dans l'ordre croissant en s'arrêtant dès que l'on a
atteint un nombre premier p tel que p2
> 1999 :
- 1999 n'est pas divisible par 2 , car il est impair
- 1999 n'est pas divisible par 3 , car la somme 1+9+9+9=28 n'est pas
divisible par trois
- 1999 n'est pas divisible par 5 , car le dernier chiffre (9) est
différent de 0 ou 5
- en effectuant des divisions euclidiennes, on constate que 1999
n'est divisible ni par 7 , ni par 11, 13, 17, 19, 23, 29, 31, 37, 41 ou
43.
- le nombre premier suivant, 47, vérifie 472 > 1999 car 472 =2209
En conclusion, 1999 est bien un nombre premier.
copyright
© School Angels 2000