Correction du sujet : Bac S 1999 Inde (Juin 99)

Exercice 2 (4 points) Énoncé

1. a. 1. b. 2. a. 2. b. 3. a. 3. b.

Ce sujet nécessite de connaître les points suivants du cours :

• barycentre
• géométrie dans le plan

On considère un triangle ABC du plan.

1. a. Déterminer et construire le point G, barycentre de [(A;1) ; (B;-1) ; (C;1)] . (0,5 point)

Le point G , par définition d'un barycentre, vérifie :

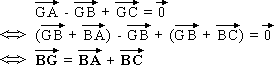
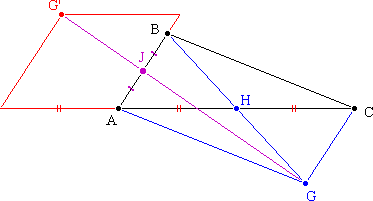
donc G est le dernier sommet du parallélogramme construit avec les segments [AB] et [AC] .

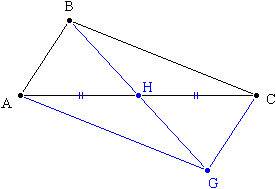
Remarque :

Soit H le milieu du segment [AC] , on a  .

1. b. Déterminer et construire le point G', barycentre de [(A;1) ; (B;5) ; (C;-2)] . (0,5 point)

On a, toujours par définition du barycentre :

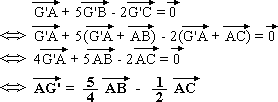
et G' se construit alors à partir de cette expression.

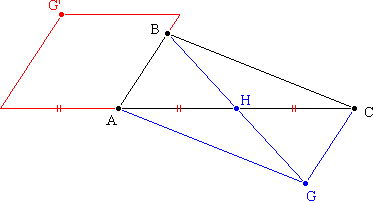
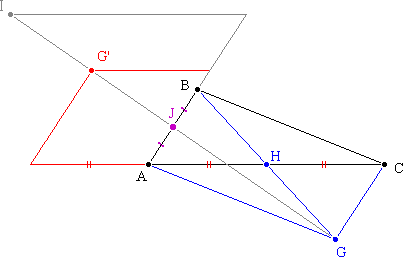
2. a. Soit J le milieu de [AB].

Exprimer et en fonction de et , et en déduire l’intersection des droites (GG') et (AB). (0,75 point ; 0,75 point)

• Comme on l'a vu à la question 1. a. , GABC est un parallélogramme, donc on a :

On peut alors écrire, en reprenant le résultat de la question précédente :

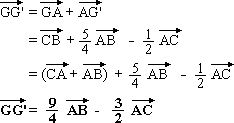
• Comme J est le milieu de [AB] , on a :

On peut alors écrire, en reprenant à nouveau le résultat de la question précédente :

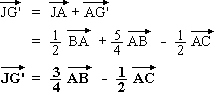
On constate immédiatement que l'on a :

donc ces deux vecteurs sont colinéaires,

donc les droites (GG') et (JG') sont parallèles et comme elles passent toutes les deux par le point G', on déduit qu'elles sont confondues,

donc les points J, G et G' sont alignés.

On sait alors que :

• la droite (GG') passe par J (cf. ci-dessus)
• la droite (AB) passe par J (car J est le milieu de [AB] !)

donc les droites (GG') et (AB) se coupent en J .

2. b. Montrer que le barycentre I de [(B;2) ; (C;-1)] appartient à (GG'). (0,5 point)

Le point I, par définition d'un barycentre, vérifie :

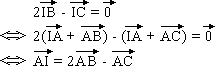
D'autre part, en utilisant ce résultat et celui de la question 2. a. , on a :

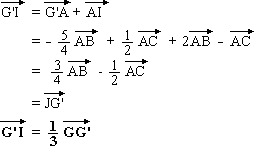
et, en utilisant exactement le même raisonnement qu'à la question précédente, on montre que les points I, G et G' sont alignés,

donc le point I appartient à la droite (GG') .

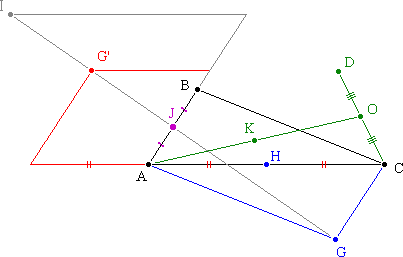
3. Soit D un point quelconque du plan. Soient O le milieu de [CD] et K le milieu de [OA].

3. a. Déterminer trois réels a, d et c tels que K soit barycentre de [(A;a) ; (D;d) ; (C;c)]. (0,5 point)

Comme O est le milieu de [CD] , on a que O est le barycentre de [(C;1) ; (D;1)] .

De même, comme K est le milieu de [OA] , K est le barycentre de [(O;1) ; (A;1)] ,

ce qui équivaut à K est le barycentre de [(O;2) ; (A;2)] .

On sait que les barycentres sont associatifs,

donc, comme :

• 1+1 = 2 (!) ,
• O est le barycentre de [(C;1) ; (D;1)] ,

le système [(O;2) ; (A;2)] équivaut au système { [(C;1) ; (D;1)] ; (A;2) } ,

ce équivaut au système [(C;1) ; (D;1) ; (A;2)] ,

donc K est le barycentre du système [(C;1) ; (D;1) ; (A;2)] ,

donc a = 2 , c = 1 et d = 1 est une solution.

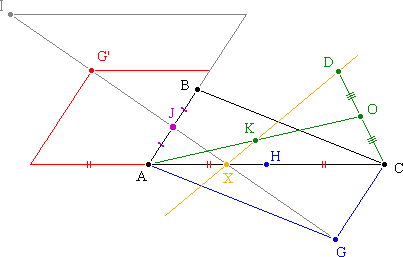
3. b. Soit X le point d’intersection de (DK) et (AC).

Déterminer les réels a' et c' tels que X soit barycentre de [(A;a') ; (C;c')]. (0,5 point)

Soit Y le barycentre du système [(A;2) ; (C;1)] , (on choisit ce point en regardant la figure ci-dessous !!!)

Y appartient alors à la droite (AC),

et comme 2+1 = 3 ( !) , K est le barycentre du système [(Y ;3) ; (D ;1)] .

donc K , Y et D sont alignés,

donc Y appartient à la droite (KD) .

En résumé, on a :

• Y appartient à la droite (AC)
• Y appartient à la droite (KD)

donc Y est le point d’intersection des droites (AC) et (KD) ,

donc le point X recherché n’est autre que le point Y,

donc X est le barycentre de [(A ;2) ; (C ;1)] ,

donc a’ = 2 et c’ = 1 est une solution.

Remarque :

On pouvait montrer ce résultat par une autre méthode, qui n’utilise pas les barycentres et qui est donc moins dans l’esprit de l’exercice, même si c’est une très belle méthode.

On a :

• K est le milieu de [OA]
• H est le milieu de [AC]

donc, d’après les propriétés de la droite des milieux dans le triangle OAC , on a que la droite (KH) est parallèle à la droite (OC) et :

Or on sait que les points D , O et C sont alignés,

donc (KH) est parallèle à (DC) .

D’autre part, O est le milieu de [DC] , donc :

On considère alors le triangle XDC et on sait que dans ce triangle, on a les propriétés suivantes :

• K appartient à (DX) ;
• H appartient à (XC) ;
• (KH) est parallèle à (DC) ;
• KH = DC / 4 ;

donc, d’après le théorème de Thalès, on a :

donc, on a :

Or ,

d’où  ,

d’où .

Or H est le milieu de [AC] ,

donc ,

donc ,

Or (relation de Chasles !),

donc ,

donc X est le barycentre de [(A ;2) ; (C ;1)] ,

donc a’ = 2 et c’ = 1 est une solution.

copyright © School Angels 2000