Correction du sujet : Bac S 1999 Asie (Juin 99)

Problème (11 points) Enoncé

Partie A : 1. 2. a. 2. b. 3. a. 3. b.

Partie B : 1. a. 1. b. 2. a. 2. b. 3.

Partie C : 1. 2. 3. 4.

Ce sujet nécessite de connaître les points suivants du cours :

• équations différentielles du premier ordre
• exponentielle
• étude de fonction
• intégration et calcul d’aire

L’objet de ce problème est de résoudre une équation différentielle, d’en étudier une fonction solution et de calculer des aires.

Partie A : Résolution de l’équation différentielle (E) : y' + y = x - 1

1. À l’aide d’une intégration par parties, calculer : (1 point)

Nous allons calculer I à l'aide d'une intégration par partie. Posons :

• u'(t) = e^t d'où u(t) = e^t
• v(t) = t - 1 d’où v'(t) = 1 .

On a alors : I = e^x(x - 1) - e^x + e .

2. a. Soit z une fonction dérivable sur l’ensemble des nombres réels. On pose f(x) = z(x) e^-x .

Montrer que la fonction f est solution de (E) si, et seulement si, pour tout x de R, z'(x) = e^x (x -1). (1 point)

f est solution de (E) si, et seulement si, pour tout réel x, f'(x) + f (x) = x - 1.

Si on pose f(x) = z(x) e^{- x} , alors f'(x) = z'(x) e^{- x} + z(x) (-e^{- x}) .

F est solution de (E) si, et seulement si, pour tout réel x :

z'(x).e^{- x} + z(x).( - e^{- x}) + z(x).e^{- x} = x - 1

z'(x) . e^{- x} = x - 1

d'où : z'(x) = e^x(x - 1) .

2. b. À l’aide de la première question, déterminer toutes les fonctions z vérifiant, pour tout x de R, z'(x) = e^x (x -1). (0,5 point)

Par la question 2. a. , on a :

z'(x) = e^x(x - 1) donc :

d'où z(x) = e^x(x -1) - e^x + k , où k désigne une constante réelle.

3. a. Déduire de la question précédente les solutions de (E). (0,5 point)

On a :

• z(x) = e^x(x -1) - e^x + k (cf. question précédente)
• f(x) = z(x) e^{- x} , (par hypothèse, cf. question 2. a.) ,

On en déduit que les fonctions solutions de (E) sont de la forme :

f(x) = [e^x(x - 1) - e^x + k] e^{- x} où k désigne une constante réelle.

3. b. Déterminer la solution de (E) pour laquelle l’image de 1 est 0. (0,5 point)

La solution de (E) pour laquelle f(1) = 0 vérifie :

(- e + k) e^-1 = 0 , d'où k = e ,

donc la solution de (E) qui s’annule en 1 est la fonction :

Partie B : Étude d’une fonction

Soit f la fonction définie sur par f(x) = x - 2 + e^1-x. Le plan est rapporté à un repère orthonormal ( O ; i , j ) (unité graphique : 1 cm). On désigne par (C_f) la courbe représentative de f .

1. a. Étudier le sens de variation de f. (1 point)

On remarque tout de suite que f n'est autre que la solution particulière de (E) obtenue à la fin de la Partie A !

Pour tout réel x , nous avons : f ’(x) = 1 - e^1-x .

Etudions le signe de cette dérivée :

f ’(x) = 1 - e^{1 - x} > 0 ó e^{1 - x} < 1

ó 1 - x < 0

ó x > 1 .

Par le même raisonnement on a : f ’(x) = 1 - e^1-x < 0 ó x < 1 et f ’(x) = 1 - e^{1 - x} = 0 ó x = 1 ,

d'où :

• f est strictement croissante sur [1 ; + ¥[ ,
• f est strictement décroissante sur ] - ¥ ; 1] .

1. b. Préciser lim _x®-¥ f(x) et lim _x®+¥ f(x) . (1 point)

Limite de f(x) en - ¥ :

Nous avons, pour tout réel non nul x : f(x) = x - 2 + e^{1 - x} = x - 2 + e/e^x .

Or :

· lim _x®-¥ e^x = 0 , donc par le théorème sur les limites de composées de fonctions, on a lim _x®-¥ 1/e^x = +¥ , d'où lim _x®-¥ e/e^x = +¥ .

· lim _x®-¥ x = - ¥.

Nous obtenons une forme indéterminée du type "¥-¥" . Pour lever cette indétermination, factorisons par x :

x - 2 + e^{1 - x} = x - 2 + e/e^x = x [1 - 2/x + e/(x.e^x)] .

On a alors :

· lim _x®-¥ (1 - 2/x) = 1 ,

· par le cours, on sait que lim _X®+¥ e^X/X = + ¥ et en faisant le changement de variables X=-x , on a e^X/X = e^-x/(-x) = -1/(x.e^x) ,

donc lim _x®-¥ 1/(x.e^x) = - ¥ ,

donc d'après les théorèmes algébriques de calcul de limites, on a :

lim _x®-¥ f(x) = +¥ .

Limite de f(x) en + ¥ :

On a :

· lim _x®+¥ x-2 = +¥ , donc par le théorème sur les limites de composées de fonctions, on a lim _x®-¥ 1/e^x = +¥ , d'où lim _x®-¥ e/e^x = +¥ .

· lim _x®+¥ e/e^x = 0.

donc d'après les théorèmes algébriques de calcul de limites, on a :

lim _x®+¥ f(x) = +¥.

2. a. Montrer que la droite (D), d’équation y = x - 2 , est asymptote à la courbe (C_f). (1 point)

Nous avons : f (x) - (x-2) = e^1-x avec lim _x®+¥ e^1-x = 0 .

donc la droite (D) d’équation y = x - 2 est asymptote à la courbe (C_f) au voisinage de +¥.

2. b. Préciser la position de (C_f) par rapport à (D). (0,5 point)

Comme pour tout x de , on a f(x) - (x-2) = e^1-x avec e^1-x > 0 ,

la courbe (C_f) est toujours située au-dessus de la droite (D).

3. Tracer (D) et (C_f). (1 point)

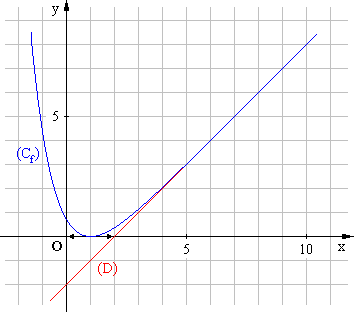
Partie C : Calcul d’aire

Soit x₀ un nombre réel strictement positif.

1. On considère le domaine limité par la courbe (C_f), son asymptote (D) et les droites d’équations x = 0 et x = x₀.

Exprimer, à l’aide de x₀, l’aire S₁ de ce domaine. (0,5 point)

L’aire S₁ en unités d’aire, de la portion de plan définie ci-dessus est donnée par

2. On considère la fonction g , définie sur par g(x) = e^{1 - x} , dont on trouvera la courbe représentative (C_g) en annexe. Donner une interprétation, en terme d’aire, de l’intégrale ayant servi au calcul de S₁ à l’aide de la courbe (C_g). (0,5 point)

L’intégrale S₁ représente l’aire (en unités d'aire) de la portion de plan délimitée, sur le graphique fourni, par la courbe représentative de la fonction g et les droites d’équations x = 0 et x = x₀ :

• 0 £ x £ x₀
• 0 £ y £ g(x)

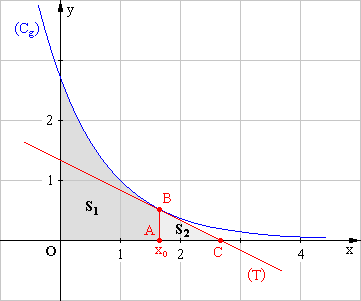
3. A est le point de coordonnées (x₀ ; 0) ; B est le point de la courbe (C_g) d’abscisse x₀.

Soit (T) la tangente à la courbe (C_g) au point d’abscisse x₀ ; C est le point d’intersection de (T) et de l’axe des abscisses.

Déterminer les coordonnées de C. (1 point)

Tout d'abord, calculons l'équation de (T). La tangente au point d’abscisse x₀ à la courbe représentative de g est donnée par :

y = g(x₀) + g'(x₀) (x - x₀)

Ona :

• g(x₀) = e^1-x0
• g'(x₀) = - e^1-x0

d'où :

(T) : y = e^1-x0 - e^1-x0 (x - x₀)

Maintenant, calculons les coordonnées du point d'intersection de (T) avec l'axe des abscisses. Il faut résoudre le systême suivant :

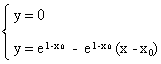
On a donc :

e^1-x0 - e^1-x0 . (x - x₀) = 0

e^1-x0 = e^1-x0 . (x - x₀)

1 = x - x₀ (car une exponentielle n'est jamais nulle, d'où e^1-x0 ¹ 0)

x = 1 + x₀ .

Le point C a donc pour coordonnées (0 ; 1+x₀) .

4. Calculer (en unités d’aire) l’aire S₂ du triangle ABC. (0,5 point)

Vérifier que S₁ + 2 S₂ = e . (0,5 point)

Les deux points A et C sont sur l'axe des abscisses et ils formeront la base du triangle ABC dans notre raisonnement. On calcule l'aire d'un triangle en divisant par deux le produit de la base par la hauteur. La hauteur correspondant à la base choisie est égale à la distance entre B et l'axe (Ox), cette distance valant g(x₀) = e^1-x0 d'où :

Nous avons donc S₂ = (e^1-x0 )/2 .

On a :

S₁ + 2S₂ = (e - e^1-x0) = e ,

donc on a bien :

S₁ + 2S₂ = e .

copyright © School Angels 2009