Correction du sujet : Bac S 1999 Antilles
- Guyane (Juin 99)
Exercice
2 (5 points) SPECIALITE Énoncé
Ce sujet nécessite de connaître les points suivants
du cours :
- nombres complexes
- théorème de Gauss
Dans le plan muni d’un repère orthonormal
(O,i,j) , on donne le point A(12;18). On désigne par B un point de l’axe (O,i)
et par C un point de l’axe (O,j) tels que :
![]()
On appelle x l’abscisse de B et y
l’ordonnée de C.
1. Démontrer que le couple (x ; y) est
solution de l’équation (E) : 2x + 3y = 78. (1 point)
Deux méthodes sont possibles : par le théorème de
Pythagore, ou par le produit scalaire.
- 1ère méthode :
Le triangle ABC est
rectangle car le sommet A représente un angle droit (-p/2, cf. énoncé) .
On peut donc appliquer le
théorème de Pythagore : AB2
+ AC2 = BC2 , et on a :
·
AB2 = (xB-xA)2
+ (yB-yA)2 = (x-12)2 + (0-18)2
= (x - 12)2 + (18)2
·
AC2
= (xC-xA)2 + (yC-yA)2
= (0-12)2 + (y-18)2 = (12)2 + (y-18)2
·
BC2
= (xC-xB)2 + (yC-yB)2
= (0-x)2 + (y-0)2 = x2 + y2
donc :
AB2 + AC2
= BC2 ó (x-12)2
+ (18)2 + (12)2 + (y-18)2 = x2
+ y2
ó x2
- 12x + 144 + 324 + 144 + y2 - 36y + 324 = x2 + y2
ó -24x -36y = -936
ó 2x + 3y = 78
donc le couple (x ; y) est
bien solution de l’équation (E).
- 2ème méthode :
On a les coordonnées
suivantes de vecteurs :
![]()
![]()
Or ces deux vecteurs sont
orthogonaux car ils forment un angle de -p/2 , donc leur produit scalaire est
nul et on a :
(x-12)(-12) + (-18)(y-18) =
0 ó 2(x-12) + 3(y-18) = 0
ó 2x
+ 3y = 2´12 + 3´18
ó 2x
+ 3y = 78
donc le couple (x ; y) est
bien solution de l’équation (E).
2. On se propose de trouver tous les
couples (B, C) de points ayant pour coordonnées des nombres entiers relatifs.
2. a. Montrer que l’on est ramené à
l’équation (E), avec x et y appartenant à l’ensemble ![]() des nombres entiers relatifs. (1 point)
des nombres entiers relatifs. (1 point)
On a
:
![]()
donc
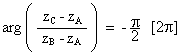
donc il existe un réel m strictement positif tel que
:
![]()
ó iy - 12 - 18i = - mi (x - 12 - 18i)
ó iy - 12 - 18i = - mix + 12mi -
18m
ó 18m - 12 + i(y + mx - 12m -
18) = 0
Pour qu'un complexe soit nul, il faut et il suffit
que partie réelle et imaginaire soient nulles.
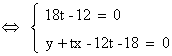
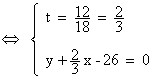
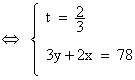
On est donc bien ramené à l’équation (E), avec x et
y appartenant à l’ensemble ![]() des nombres entiers relatifs (afin que les
coordonnées de A et B soient des entiers relatifs).
des nombres entiers relatifs (afin que les
coordonnées de A et B soient des entiers relatifs).
2. b. À partir de la définition de B et
C, trouver une solution particulière (x0 ; y0) de (E)
avec x0 et y0 appartenant à ![]() . (1
point)
. (1
point)
Deux méthodes sont encore possibles : la première
est géométrique, la seconde algébrique et moins jolie.
La définition de B et C
équivaut à :
·
B
appartient à l'axe (O,i)
·
C
appartient à l'axe (O,j)
·
ABC
est rectangle en A
Si on considère B comme la
projection orthogonale de A sur (O,i) , et C comme la projection orthogonale
de A sur (O,j) , alors le triangle ABC est bien rectangle en A,
donc les points B0(12;0)
et C0(0;18) conviennent,
donc le couple (x0;y0)
= (12;18) est une solution particulière de l'équation (E) .
- 2ème méthode :
Par la question 1. ,
on a (E) : 2x + 3y = 2´12 + 3´18 = 78 .
donc le couple (x0;y0)
= (12;18) est une solution particulière de l'équation (E).
2. c. Démontrer qu’un couple (x;y)
d’entiers relatifs est solution de l’équation (E) si, et seulement si, il est
de la forme (12+3k ; 18-2k), où k appartient à ![]() . (1
point)
. (1
point)
Nous avons :
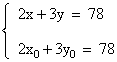
Effectuons la soustraction membre à membre de ces
deux équations :
ó 2(x
- 12) + 3(y - 18) = 0 ó
2(x - 12) = - 3(y - 18)
Comme 2 divise
2(x-12) , il divise aussi
3(y-18) .
Or 2 et 3 sont premiers entre eux,
donc, par le théorème de Gauss, 2 divise y-18 ,
donc il existe p entier relatif tel que : y-18 = 2p ,
d'où
2(x-12) = -3.(2p) ó
x-12 = -3p ,
donc les solutions de E dans ![]() sont tous les couples d'entiers relatifs de
la forme (12-3p , 18+2p) , p
appartenant à
sont tous les couples d'entiers relatifs de
la forme (12-3p , 18+2p) , p
appartenant à ![]() ,
,
et en posant k = -p , on a que les solutions de E
dans ![]() sont tous les couples d'entiers relatifs de
la forme (12+3k , 18-2k) , k
appartenant à
sont tous les couples d'entiers relatifs de
la forme (12+3k , 18-2k) , k
appartenant à ![]() .
.
2. d. Combien y a-t-il de couples de
points (B, C) ayant pour coordonnées des nombres entiers relatifs, tels
que -6 £ x £ 21 et
-5 £ y £ 14 ? (1,5
point)
Par la question précédente, on doit en fait trouver
les entiers relatifs k tels que : -6 £ 12+3k £ 21 et
-5 £ 18-2k £ 14 .
donc :
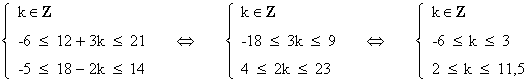
On obtient alors
k = 2 ou k = 3 .
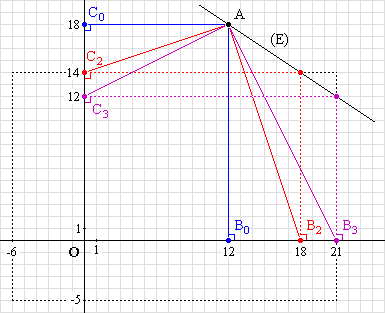
Il y a donc deux couples de points (B,C) ayant pour
coordonnées des entiers relatifs, tels que
-6 £ x £ 21 et
-5 £ y £ 14 .
Ces couples sont :
- k = 2 : B2(18,0) et C2(0,14)
- k = 3 : B3(21,0) et C3(0,12)
copyright
© School Angels 2000