School Angels

Correction du sujet : Bac L 1999 Maroc (Juin 99)

Exercice 1 (4 points) SPECIALITE Énoncé

1. 2. a. 2. b. 3. 4. 5.

Ce sujet nécessite de connaître les points suivants du cours :

arbre pondéré
probabilités usuelles

Trois joueurs désignés par J₁, J₂ et J₃ ont chacun en main 4 jetons indiscernables au toucher :

· J₁ a en main 2 jetons rouges et 2 jetons noirs ;

· J₂ a en main 1 jeton rouge et 3 jetons noirs ;

· J₃ a en main 3 jetons rouges et 1 jeton noir.

Pour jouer une partie, chaque joueur choisit au hasard (sans regarder) un de ses jetons et le pose devant lui. Un joueur gagne si, et seulement si, les conditions suivantes sont réalisées :

· ses deux adversaires ont posé un jeton de même couleur ;

· son propre jeton est de couleur différente.

1. Expliquer pourquoi il y a zéro ou un joueur gagnant. (0,5 point)

On ne peut obtenir que des triplets (= série de trois) de jetons avec deux couleurs (l’ordre ne rentre pas en compte). Etudions les cas possibles et le nombre de vainqueur :

(N,N,N) il n’y a pas de vainqueur
(R,N,N) le joueur qui a posé le jeton rouge (R) est vainqueur
(R,R,N) le joueur qui a posé le jeton noir (N) est vainqueur
(R,R,R) il n’y a pas de vainqueur

donc, soit il n’y a pas de vainqueur, soit le vainqueur est unique.

On peut aussi raisonner avec un arbre pondéré :

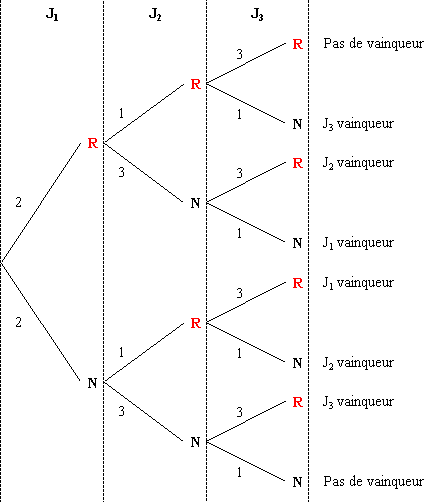
On retrouve bien qu’il y a zéro ou un joueur gagnant.

2. Calculer la probabilité des événements suivants :

2. a. E₁ : “ J₁, J₂ et J₃ posent chacun un jeton rouge ”. (0,5 point)

On a :

J₁ ayant 2 jetons rouges et 2 jetons noirs la probabilité que J₁ dépose un jeton rouge est 2/4 = 1/2
J₂ ayant 1 jeton rouge et 3 jetons noirs la probabilité que J₂ dépose un jeton rouge est 1/4
J₃ ayant 3 jetons rouges et 1 jeton noir la probabilité que J₃ dépose un jeton rouge est 3/4

Les tirages de jetons par chacun des joueurs s’effectuant de façon indépendante, on en déduit :

La probabilité que les joueurs posent chacun un jeton rouge est égale à 3/32 .

2. b. E₂ : “ J₁, J₂ et J₃ posent chacun un jeton noir ”. (0,5 point)

Utilisons le même raisonnement que ci-dessus. On a :

J₁ ayant 2 jetons rouges et 2 jetons noirs la probabilité que J₁ dépose un jeton noir est 2/4 = 1/2
J₂ ayant 1 jeton rouge et 3 jetons noirs la probabilité que J₂ dépose un jeton noir est 3/4
J₃ ayant 3 jetons rouges et 1 jeton noir la probabilité que J₃ dépose un jeton noir est 1/4

Chaque joueur posant indépendamment des deux autres un jeton devant lui, on en déduit que la probabilité de E₂ est :

La probabilité que les joueurs posent chacun un jeton noir est aussi égale à 3/32 .

3. En déduire la probabilité de l’événement N : “ il n’y a pas de joueur gagnant ”, puis celle de l’événement V : “ il y a un joueur gagnant ”. (1 point)

L’événement N est réalisé si :

les trois joueurs ont déposé un jeton rouge (événement E₁)
les trois joueurs ont déposé un jeton noir (événement E₂).

Les évènements E₁ et E₂ étant incompatibles, on en déduit que :

p(N) = p(E₁) + p(E₂)

La probabilité qu’il n’y ait pas de joueur gagnant est donc égale à 3/16 .

V est l’événement contraire de N, donc :

p(V) = 1 - p(N)

La probabilité qu’il y ait un vainqueur est donc égale à 13/16 .

4. Calculer la probabilité de l’événement A : “ il y a un joueur gagnant et c’est J₂ ”. (0,5 point)

A est réalisé dans deux cas :

J₂ a posé un jeton rouge et J₁ et J₃ ont posé un jeton noir. La probabilité de cet événement est :

J₂ a posé un jeton noir et J₁ et J₃ ont posé un jeton rouge. La probabilité de cet événement est :

Ces deux événements étant incompatibles, on en déduit :

La probabilité que J₂ gagne est égale à 5/16 .

5. Sachant qu’il y a un gagnant, calculer la probabilité que ce soit J₂. (1 point)

La probabilité que J₂ gagne sachant qu’il y a un gagnant est en fait : p(A/V) . On a alors :

On a de plus : p(AÇV) = p(A) (en effet, s’il y a un gagnant et que J₂ gagne, cela revient à ce que J2 gagne, tout simplement !), donc :

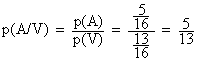
donc la probabilité que le joueur J₂ gagne sachant qu’il y a un gagnant est égale à 5/13 .