Correction du sujet : Bac ES 1999 Paris (Juin 99)
Exercice
2 (5 points) Énoncé
1. a. 1. b. 2. a. 2. b. 2. c. 2. d. 3.
Ce sujet nécessite de
connaître les points suivants du cours :
- lecture graphique
- inverse d’une fonction
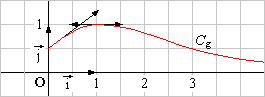
La courbe ci-dessous représente une fonction f définie et dérivable sur [0 ; +¥[ dans le repère (O; i , j ) .
On note f ' la fonction dérivée de f .
La droite (TA) est la tangente au point A d’abscisse 0.
La courbe admet une tangente parallèle à l’axe des abscisses au point d’abscisse 1.
Enfin, la fonction f est croissante sur [1 ; +¥[ et sa limite en +¥ est +¥ .
1. À partir des informations portées sur le graphique et complétées par les précisions précédentes, répondre aux questions suivantes :
1. a. Reproduire et compléter le tableau ci-dessous : (1 point)
|
x |
0 |
1 |
|
f(x) |
|
|
|
f ’(x) |
|
|
A partir du graphe on observe et on déduit ce qui
suit.
La courbe représentative de f passe par le point A
de coordonnées (0,2) ,
donc f(0) = 2
.
La tangente en A a pour coefficient directeur -3 et,
d’après le cours, on sait que le coefficient directeur de la tangente est égal
à la valeur de la dérivée de la fonction au point de tangence,
donc f ’(0) = -3
.
La courbe représentative de f passe par le point de
coordonnées (1,1) ,
donc f(1) = 1
.
La tangente en ce point est horizontale , donc son
coefficient directeur est 0 ,
donc f ’(1) = 0
.
On déduit de ceci le tableau suivant :
|
x |
0 |
1 |
|
f(x) |
2 |
1 |
|
f
’(x) |
-3 |
0 |
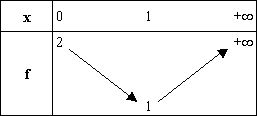
1. b. Donner le tableau de variation de f sur [0 ; + ¥ [, complété par la limite en + ¥. (0,5 point)
On déduit du graphe donné dans l’énoncé le tableau
de variation suivant pour la fonction f :
2. On considère la fonction g inverse de la fonction f, c’est-à-dire g = 1/f .
On note g¢, la fonction dérivée de g.
2. a. Déterminer g(0), g(1), g(3). (0,75 point)
On
a :
![]()
![]()
![]()
2. b. Quel est le sens de variation de la fonction g sur [0 ; +¥[ ? Justifier la réponse donnée. (0,5 point)
Comme g = 1/f
et que pour tout x de [0 ; +¥[ , f(x) n’est jamais nul,
on a :
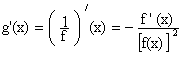
donc le signe de g’ est l’opposé de celui de f ’ .
Or on sait que :
- f est strictement positive et décroissante sur [0 ; 1[ ;
- f est strictement positive et croissante sur [1 ; +¥[ ;
donc :
- g est croissante sur [0 ; 1[ ;
- g est décroissante sur [1 ; +¥[ .
2. c. Déterminer les valeurs g’(0) ,
g’(1) . (0,75 point)
On
a :
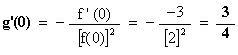
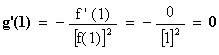
2. d. Déterminer la limite de g en +¥ . (0,25 point)
On a lim x®+¥ f(x) = +¥ , donc lim x®+¥ [ 1/f(x) ] = 0 .
Or, pour tout x de [0 ; +¥[ , on a g(x) = 1/f(x) ,
d’où lim x®+¥ g(x) = 0 .
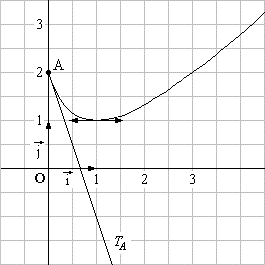
3. On souhaite traduire graphiquement les informations obtenues pour la fonction g .
Tracer une courbe qui satisfait aux résultats obtenus à la question 2, dans un repère orthonormal (unité 2 cm) sur une feuille de papier millimétré ; le tracé des tangentes aux points d’abscisses 0 et 1 devra apparaître sur la figure. (1,25 point)
Courbe représentative de g