School Angels

Correction du sujet : Bac ES 1999 Amérique du Nord (Juin 99)

Problème (10 points) Énoncé

Partie A : 1. 2. 3. a. 3. b. 4.

Partie B : 1. 2. 3. a. 3. b. 3. c.

Ce sujet nécessite de connaître les points suivants du cours :

· statistiques

· coefficient de corrélation linéaire

· ajustement affine

· logarithme népérien

Une entreprise envisage la fabrication d’un nouveau produit. Sa décision dépend des résultats de plusieurs études :

Étude de la demande pour ce nouveau produit : c’est l’objet de la partie A.

Étude d’un coût moyen de production : c’est l’objet de la partie B.

Partie A :

Une étude a permis d’établir le tableau suivant où, pour différentes observations, x_i désigne la quantité de produit (en milliers d’unités) que la clientèle est disposée à acheter, et y_i le prix de vente (en francs) d’une unité :

x_i	1,5	3	5	8	11	12
y_i	120	110	100	90	80	70

Ainsi, pour que la clientèle soit disposée à acheter 5000 unités, le prix de vente d’une unité doit être fixé à 100 F.

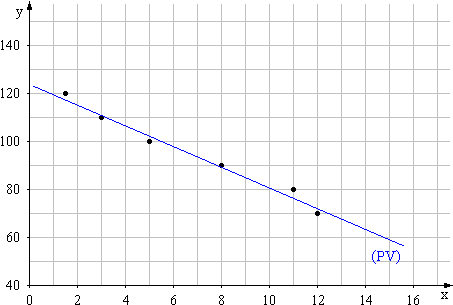
1. Représenter le nuage de points associé à cette série statistique. (0,5 point)

Prendre 1 cm pour 1 millier d’unités en abscisse, et 1 cm pour 10 francs en ordonnée.

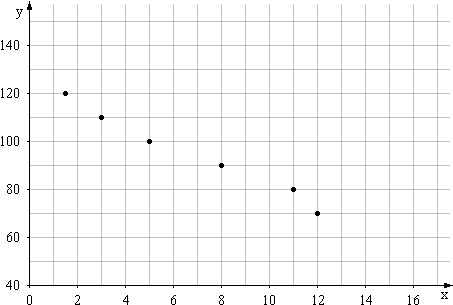
Dans les questions suivantes, le détail des calculs statistiques n’est pas demandé ; les résultats seront donnés à 10^-2 près.

Les calculs ne sont pas demandés, mais ils sont donnés dans la suite à titre indicatif.

2. Donner le coefficient de corrélation linéaire de cette série statistique. (1 point)

Un ajustement affine est-il approprié ? Justifier la réponse. (0,5 point)

Le coefficient de corrélation linéaire se calcule à l’aide de la formule :

Avec :

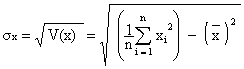
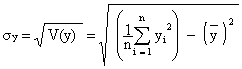
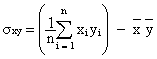
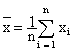
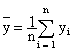
On a alors :

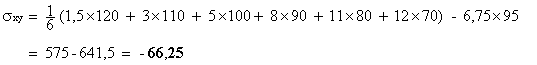
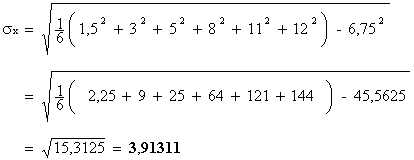
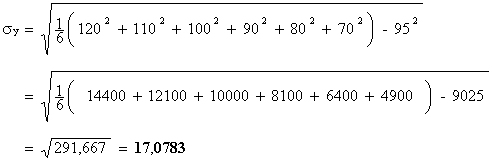
d’où :

Le coefficient de corrélation linéaire de la série statistique {( x_i ; y_i)} est égal à -0,99 à 10 ^- ² près.

L’ajustement affine est justifié puisque r est très proche de –1 .

3. a. Donner une équation de la droite d’ajustement de y en x, obtenue par la méthode des moindres carrés. (1 point)

Une équation de la droite d’ajustement de y en x , obtenue par la méthode des moindres carrés est y = a x + b , avec :

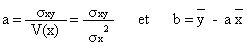
On a alors :

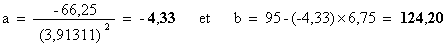
Une équation de la droite d’ajustement de y en x par la méthode des moindres carrés est donc :

y = - 4,33x + 124,20.

3. b. D’après ce modèle, comment faut-il fixer le prix de vente d’une unité si l’on veut pouvoir vendre un minimum de 6500 unités ? (1 point)

Si l’on veut pouvoir vendre au moins 6500 unités du produit, alors on doit avoir x £ 6,5 .

donc - 4,33 x £ - 4,33 ´ 6,5

donc - 4,33 x + 124,20 £ - 4,33 ´ 6,5 + 124,20

donc y = - 4,33 x + 124,20 £ - 4,33 ´ 6,5 + 124,20 £ 96,055

Le prix de vente en francs d’une unité doit donc être inférieur ou égal à 96,05 francs si l’on souhaite vendre au moins 6500 unités.

4. On admet que le prix de vente d’une unité, noté PV, est une fonction de la demande x (en milliers d’unités) définie, pour x Î [2 ; 15], par :

PV (x) = - 4,33 x + 124,2.

Représenter la fonction PV dans le repère utilisé dans la question 1. (0,5 point)

Comme par hasard, l’expression de PV est celle de la droite obtenue à la question précédente !

Partie B :

Le coût total de production (en francs) de x milliers d’unités est, pour x Î [2 ; 15] :

CT(x) = 10⁵ [x + 4 - 3 ln(x)]

et le coût moyen de production d’une unité est, pour x Î [2 ; 15] :

1. On note CM’ la dérivée de la fonction CM.

Calculer CM’(x) et démontrer que CM’(x) a le même signe que ln(x) - 7/3 , pour tout x Î [2 ; 15]. (1,5 point)

La fonction CM est dérivable sur [2 ; 15] en tant que quotient :

de fonctions dérivables sur [2 ; 15] ;
dont le dénominateur ne s’annule pas sur [2 ; 15] .

On pose, pour tout x Î [2 ; 15] :

u(x) = CT(x) d’où u’(x) = CT’(x)
v(x) = 1000 x d’où v’(x) = 1000

On peut ainsi écrire, pour tout x Î [2 ; 15] f = u/v d’où : f ’ = (u’v - uv’) / v ² ,

d’où :

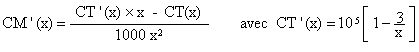
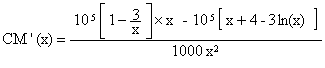
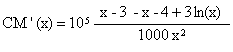
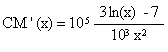
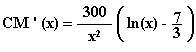
Or, pour tout x Î [2 ; 15] , on a : 300/x² > 0

donc CM’(x) est du signe de ln(x) – (7/3) sur [2 ; 15] .

2. Résoudre sur l’intervalle ]0 ; +¥[ l’inéquation ln(x) - 7/3 ³ 0 . (1 point)

On a :

ln(x) – (7/3) ³ 0 ó ln(x) ³ 7/3

ó x ³ e^7/3 (car la fonction exponentielle est croissante sur ]0 ; +¥[ )

L’inéquation ln(x) – (7/3) ³ 0 admet donc pour solution l’ensemble [e^7/3 ; +¥[ .

3. a. Étudier les variations de CM sur l’intervalle [2 ; 15]. (1 point)

On a : e^7/3 = 10,3 à 0,1 près, donc e^7/3 Î [ 2 ; 15].

A partir des résultats obtenus aux questions précédentes, on en déduit le tableau de variations de CM .

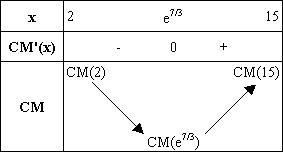
Avec :

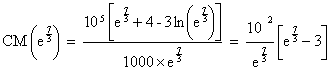
3. b. Tracer la représentation graphique de CM dans le repère utilisé dans la partie A. (1 point)

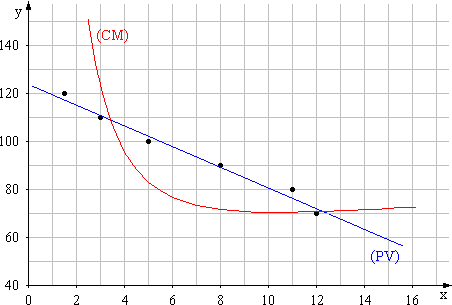
3. c. À l’aide du graphique, déterminer l’ensemble des valeurs de x pour lesquelles l’entreprise peut faire un bénéfice. (On donnera la réponse sous forme d’un intervalle dont les bornes sont des entiers.) (1 point)

L’entreprise réalisera un bénéfice si le prix de vente à l’unité est supérieur au coût moyen de production d’une unité. Il faut donc déterminer les intervalles sur lesquels la courbe représentative de PV est située au-dessus de la courbe représentative de CM .

Par une lecture graphique, on déduit que l’ensemble des valeurs de x pour lesquelles l’entreprise peut faire un bénéfice est l’intervalle [4 ; 12] .