School Angels

Correction du sujet : Bac ES 1999 Antilles - Guyane (Juin 99)

Problème (10 points) Énoncé

Partie A : 1. 2. 3.

Partie B : 1. 2. 3. 4.

Partie C : 1. 2. 3.

Ce sujet nécessite de connaître les points suivants du cours :

· logarithme népérien

· étude de fonction

· intégration et calcul d’aire

Le but du problème est l’étude d’une fonction et le calcul d’une aire liée à cette fonction.

Partie A

La courbe (G) ci-jointe est la représentation graphique dans un repère orthonormal d’une fonction g définie et dérivable sur. ]0 ; +¥[

Les points A (1 ; 3/2) et B (e ; e²/2) appartiennent à la courbe (G) et la tangente en A à (G) est parallèle à l’axe des abscisses.

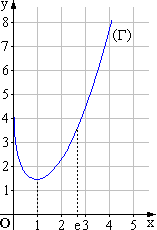
1. Déterminer g(1) , g(e) et g’(1). (1 point)

On a :

le point A (1 ; 3/2) appartient à (G) , donc g(1) = 3/2 .
le point B (e ; e²/2) appartient à (G) , donc g(e) = e²/2 .

Par lecture graphique, on constate que la tangente en A (abscisse x = 1) est parallèle à l’axe des abscisses. Or la pente d’une tangente à une courbe est égale à la valeur que prend la dérivée de la fonction en ce point,

donc g’(1) = 0 .

2. Déterminer les réels a et b, sachant que la fonction g est définie sur ]0 ; +¥[ par une expression de la forme : (0,75 point)

Par la question précédente, on a :

g(1) = 3/2 , d’où : 3/2 = 1/2 + a , d’où a = 1 .
g(e) = e²/2 , d’où : e²/2 = e²/2 + a + b , d’où b = -a , d’où b = -1 .

Donc, pour tout x de ]0 ; +¥[ , g(x) = x²/2 + 1 - ln x .

3. Sachant que g(x) = x²/2 + 1 - ln x , retrouver au moyen d’un calcul, le sens de variation de g . (Le calcul des limites n’est pas demandé.)

En utilisant ce dernier résultat, étudier le signe de g sur ]0 ; +¥[ . (1,25 point)

Comme par hasard, on retrouve l’expression de g obtenue à la question précédente. Moralité : toujours lire l’énoncé en entier pour voir si la réponse à une question n’est pas donnée plus loin !

La fonction g est dérivable sur ]0 ; +¥[ , en tant que somme de fonctions dérivables et on a , pour tout x de ]0 ; +¥[ ,

Pour tout x de ]0 ; +¥[ , (x+1)/x > 0 ,

donc le signe de g’(x) est celui de x - 1 ,

donc :

g’(x) > 0 sur ]0 ; 1[ ;
g’(1) = 0 ;
g’(x) < 0 sur ]1 ; +¥[ .

donc :

g est strictement décroissante sur ]0 ; 1[ ;
g est strictement croissante sur ]1 ; + ¥[ .

On déduit de ce qui précède le tableau de variations de g :

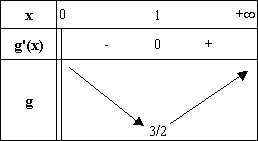
D’après le sens de variation de g , on a, pour tout x de ]1 ; +¥[ : g(x) ³ 3/2 ,

donc, pour tout x de ]1 ; +¥[ : g(x) > 0 .

Partie B

On considère la fonction f définie sur ]0 ; +¥[ par :

1. Calculer les limites de f en 0 et en +¥ . (1 point)

(On admet le résultat suivant : lim _x_®₊_¥ (ln x)/x = 0 )

On a :

lim _x_®₀₊ ln(x) = -¥
lim _x_®₀₊ 1/x = +¥

donc, d’après les théorèmes sur les opérations algébriques de limites, on a : lim _x_®₀₊ (ln x)/x = -¥ .

Or lim _x_®₀₊ x = 0 ,

donc lim _x_®₀₊ f(x) = -¥ .

Par hypothèse de l’énoncé, on a lim _x_®₊_¥ ln(x)/x = 0 .

Or lim _x_®₊_¥ x = +¥

donc lim _x_®₊_¥ f(x) = +¥ .

2. Calculer la dérivée f ' de f . (0,5 point)

Vérifier que f '(x) = g(x)/x² pour tout réel positif x. (0,5 point)

En déduire les variations de f. (0,5 point)

Définissons, pour tout x de ]0 ; +¥[ , les trois fonctions suivantes :

u(x) = ln(x)
v(x) = x
w(x) = x/2

Ces trois fonctions sont dérivables sur ]0 ; +¥[ et on a :

u’(x) = 1/x
v’(x) = 1
w’(x) = 1/2

Comme la fonction v n’est jamais nulle sur ]0 ; +¥[ , f = (u/v) + w est dérivable et on a, d’après les théorèmes de dérivations :

donc, pour tout x de ]0 ; +¥[ , on a :

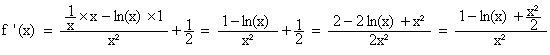
donc :

D’après le résultat de la question A. 3. , on a, pour tout x de ]0 ; +¥[ , g(x) > 0 ,

donc f ’(x) > 0 , (car x² est toujours strictement positif !)

donc f est strictement croissante sur ]0 ; +¥[ .

On déduit de ce qui précède le tableau de variations de f :

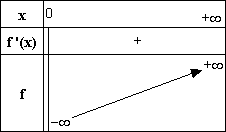
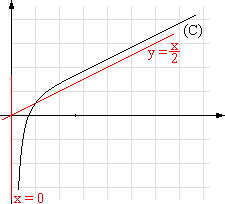
3. Montrer que la représentation graphique (C) de f dans un repère orthonormal admet deux asymptotes que l’on précisera. (1 point)

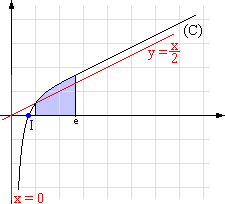
La courbe (C) de f est donnée en annexe dans un repère orthonormal (O ; i , j ), unité 2 cm sur chaque axe.

On a lim _x_®₀₊ f(x) = -¥ ,

donc la droite d’équation x = 0 est une asymptote verticale à la courbe représentative de f .

D’autre part, on a :

donc la droite d’équation y = x/2 est asymptote à la courbe représentative de f au voisinage de + ¥ .

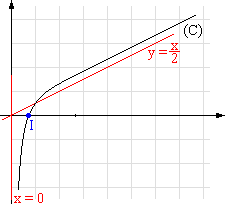
4. On admet l’existence d’un réel a unique, appartenant à [1/2 ; 1] tel que f(a) = 0 .

Que représente a pour la courbe (C) ?

Placer sur la courbe (C) le point I d’abscisse a .

Montrer que ln a = -a²/2 . En déduire que f ’(a) = (1+a²)/a² . (1,5 point)

a est l’abscisse du point d’intersection de la courbe représentative de f et de l’axe des abscisses.

On a f(a) = 0 , d’où :

Or, on a :

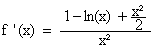
donc :

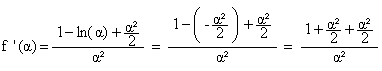
d’où :

Partie C

1. Calculer la dérivée de la fonction h définie sur ]0 ; +¥[ par h(x) = (ln x)² . (0,5 point)

La fonction logarithme népérien est définie et dérivable sur ]0 ; +¥[ . Posons t(x) = ln x , on a alors t’(x) = 1/x .

On peut alors écrire h = t² d’où, d’après les formules de dérivation, on a : h’ = 2 t t’

d’où, pour tout x de ]0 ; +¥[ , on a :

2. En déduire le calcul de J : (1 point)

Or on a h(e) = 1 et h(1) = 0 d’où :

J = 1/2

3. Hachurer sur le graphique le domaine plan limité par (C), l’axe des abscisses, et les droites d’équations x = 1 et x = e.

Déterminer l’aire, en cm², de ce domaine. (1,5 point)

L’aire (en unités d’aire) du domaine plan grisé est donnée par :

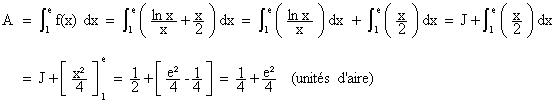
Une unité d’aire valant 2 ´ 2 = 4 cm² , on a :

A = 1+e² cm²