Correction du sujet : Bac ES 1999 Antilles - Guyane (Juin 99)
Exercice
1 (4 points) Énoncé
Ce sujet nécessite de
connaître les points suivants du cours :
- programmation linéaire
- régions du plan
Le plan est rapporté à un repère orthonormal, dont les unités sont 1 cm sur chaque axe.
Construire ce repère sur votre copie en plaçant l’origine du repère en bas et à gauche.
Partie A :
a.
Représenter la droite (D1)
d’équation 3x + y = 30, la droite (D2) d’équation
x + 4y = 30 et la
droite (D3) d’équation x + y = 10.
(0,75 point)
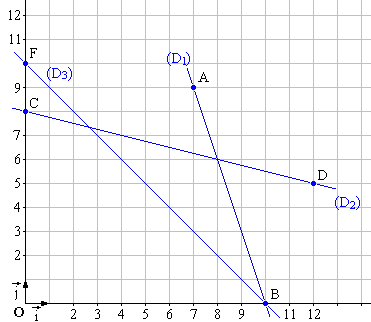
On construit le graphe ci-dessous en déterminant
pour chaque droite deux points qui leur appartiennent. Ensuite, on trace les
droites en reliant les deux points.
- (D1) : 3x + y = 30 passe par A(7;9) et B(10;0)
- (D2) : x + 4y = 32 passe par C(0 ; 8) et D(12;5)
- (D3) : x + y = 10 passe par B(10;0) et F(0;10)
b. Déterminer au moyen d’un calcul les coordonnées du point d’intersection I des droites (D1) et (D2). (1 point)
Les coordonnées du point d’intersection I des
droites (D1) et (D2) vérifient le système
suivant :
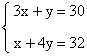
On résout ce système par substitution :
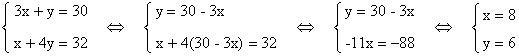
On pouvait également substituer par l’autre
inconnue :
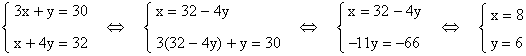
donc le point I ,
intersection des droites (D1) et (D2) , admet pour
coordonnées (8 ; 6) .
c. Repérer graphiquement à l’aide d’une croix (“ X ”) les points du plan dont les coordonnées sont des nombres entiers positifs, x et y, qui vérifient de plus les conditions : (1 point)
· 3x + y £ 30
· x + 4y £ 32
· x + y ³ 10
Il faut résoudre graphiquement le système
suivant :
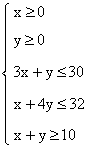
- L’inéquation x ³ 0 désigne le demi-plan situé à droite de
l’axe vertical.
- L’inéquation y ³ 0 désigne le demi-plan situé au-dessus
de l’axe horizontal.
- L’inéquation 3x + y £ 30 désigne le demi-plan délimité par (D1)
et contenant O, car les coordonnées de O vérifient cette inéquation.
- L’inéquation x + 4y £ 32 désigne le demi-plan délimité par (D2)
et contenant O, car les coordonnées de O vérifient cette inéquation.
- L’inéquation x + y ³ 10 désigne le demi-plan délimité par (D3)
et ne contenant pas O, car les coordonnées de O ne vérifient pas cette
inéquation.
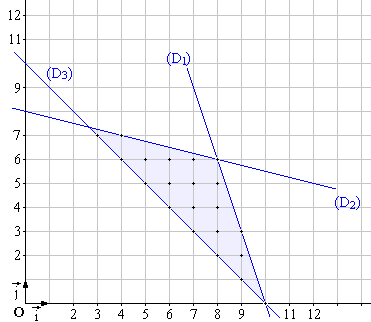
L’ensemble des points de
coordonnées entières positives (x ; y) solutions ce système est
l’intersection de ces demi-plans : la zone est représentée en bleu pale
ci-dessous. Les inégalités étant non strictes, les portions de droites qui
délimitent la zone sont inclus dedans. On obtient ainsi 21 points solutions.
Partie B :
Un artisan fabrique deux sortes de poupées : des petites poupées et des grandes poupées. Les petites poupées nécessitent 3 heures de travail et les grandes poupées une heure seulement. L’artisan, avec ses ouvriers, peut travailler 30 heures au plus par jour.
L’artisan ne dispose que de 32 mètres de tissu par jour. Il lui faut 1 mètre de tissu pour habiller une petite poupée et 4 mètres pour habiller une grande poupée.
On désigne par x le nombre de petites poupées et par y le nombre de grandes poupées produites dans une journée. L’artisan s’impose de fabriquer au moins 10 poupées par jour.
On admet que les contraintes de l’énoncé correspondent aux conditions suivantes :
· x et y sont deux nombres entiers positifs
· 3x + y £ 30
· x ³ 0 y ³ 0
· x + 4y £ 32
· x + y ³ 10.
Le nombre total de poupées produites dans une journée de travail est représenté par S = x + y.
L’artisan veut que sa production journalière S soit maximum. Combien de poupées de chaque sorte doit-il fabriquer ? (1,25 point)
Bien que cela ne soit pas demandé, montrons tout
d’abord que le problème de l’artisan se traduit bien par les contraintes de
l’énoncé.
On appelle x le nombre de petites poupées et y le nombre de grandes poupées. On ne peut pas fabriquer un nombre négatif de poupée : x et y sont des entiers naturels, donc :
- x ³ 0
- y ³ 0
Les petites poupées nécessitent 3 heures de travail
et les grandes 1 heure, donc le temps nécessaire à la fabrication de x petites
poupées et y grandes poupées est 3x + y et
comme l’artisan et ses ouvriers ne peuvent pas travailler plus de 30 heures par
jour, on en déduit que :
- 3x + y £ 30
Il faut 1 mètre de tissu pour habiller une petite
poupée et 4 mètres de tissu pour habiller une grande poupée,
donc pour habiller
x petites poupées et y
grandes poupées, il faut x +
4y mètres de tissus.
Or l’artisan ne dispose que de 32 mètres de tissu par jour, on en déduit que :
- x + 4y £ 32
L’artisan s’impose de fabriquer au moins 10 poupées
par jour, on en déduit que :
- x + y ³ 10
On a bien retrouvé touts les contraintes
données !
On remarque tout de suite que ces contraintes sont
celles de la question A. c. , donc les solutions sont les coordonnées des
points obtenus par résolution graphique à cette même question. On obtient ainsi
toutes les possibilités de production pour l’artisan.
Construisons
un tableau regroupant toutes les solutions et calculons la production totale
S :
|
x |
3 |
4 |
4 |
5 |
5 |
6 |
6 |
6 |
7 |
7 |
7 |
7 |
8 |
8 |
8 |
8 |
8 |
9 |
9 |
9 |
10 |
|
y |
7 |
6 |
7 |
5 |
6 |
4 |
5 |
6 |
3 |
4 |
5 |
6 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
0 |
|
S = x+y |
10 |
10 |
11 |
10 |
11 |
10 |
11 |
12 |
10 |
11 |
12 |
13 |
10 |
11 |
12 |
13 |
14 |
10 |
11 |
12 |
10 |
On en déduit que la production S est maximum lorsque l’artisan fabrique 8 petites poupées et 6 grandes poupées.
copyright © School Angels 2000